题目内容
5.设函数f(x)=ax-sinx,x∈[0,π].(1)当a=$\frac{1}{2}$时,求f(x)的单调区间;
(2)若不等式f(x)≤1-cosx恒成立,求实数a的取值范围.
分析 (1)当a=$\frac{1}{2}$时,f(x)=$\frac{1}{2}$x-sinx,x∈[0,π],从而求导f′(x)=$\frac{1}{2}$-cosx,从而判断函数的单调性;
(2)化简可得ax-sinx≤1-cosx,作函数y=ax-1与函数y=sinx-cosx的图象,结合图象求解即可.
解答 解:(1)当a=$\frac{1}{2}$时,f(x)=$\frac{1}{2}$x-sinx,x∈[0,π],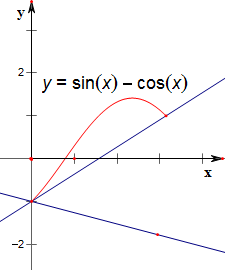
f′(x)=$\frac{1}{2}$-cosx,
故x∈[0,$\frac{π}{3}$)时,f′(x)<0,x∈($\frac{π}{3}$,π]时,f′(x)>0;
故f(x)在[0,$\frac{π}{3}$)上是减函数,在[$\frac{π}{3}$,π]上是增函数;
(2)由题意得,
ax-sinx≤1-cosx,
故ax-1≤sinx-cosx,
作函数y=ax-1与函数y=sinx-cosx的图象如图,
结合图象可得,
a≤$\frac{1-(-1)}{π-0}$=$\frac{2}{π}$;
故实数a的取值范围为(-∞,$\frac{2}{π}$].
点评 本题考查了导数的综合应用及数形结合的思想应用,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15.设0<b<a<1,则下列不等式不成立的是( )
| A. | 2b<2a<2 | B. | $0<{log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}$b | ||
| C. | ab<b2<1 | D. | ab<a2<1 |