题目内容
20.设x,y满足约束条件$\left\{\begin{array}{l}x+y≥3\\ x-y≥-1\\ 2x-y≤3\end{array}\right.$,若目标函数z=abx+y(a>0,b>0)的最大值为8,则a+b的最小值为$\sqrt{3}$.分析 作出不等式对应的平面区域,利用线性规划的知识先求出a,b的关系,然后利用基本不等式求a+b的最小值.
解答 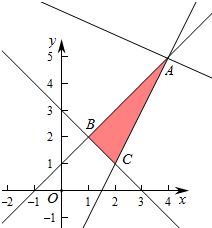 解:由z=abx+y(a>0,b>0)得y=-abx+z,
解:由z=abx+y(a>0,b>0)得y=-abx+z,
作出可行域如图:
∵a>0,b>0,
∴直线y=-abx+z的斜率为负,且截距最大时,z也最大.
平移直线y=-abx+z,由图象可知当y=-abx+z经过点A时,
直线的截距最大,此时z也最大.
由$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,即A(4,5).
此时z=4ab+5=8,
即ab=$\frac{3}{4}$,
则a+b$≥2\sqrt{ab}$=2$\sqrt{\frac{3}{4}}$=$\sqrt{3}$,
当且仅当a=b=$\frac{\sqrt{3}}{2}$时取=号,
故最小值为$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查线性规划的应用以及基本不等式的应用,利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
10.若tanα=1,α∈(0,$\frac{π}{2}})$),则sinα•cosα=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
11.关于函数y=4x2+$\frac{1}{x}$在x∈(0,+∞)上的最值的说法,下列正确的是( )
| A. | 最大值为3,无最小值 | B. | 无最大值,最小值为3 | ||
| C. | 无最大值,无最小值 | D. | 无最大值,最小值为$\frac{33}{2}$ |
8.等差数列{an}前n项和为Sn且满足S17>0,S18<0,则$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,…$\frac{{S}_{17}}{{a}_{17}}$中最小项是( )
| A. | $\frac{{S}_{8}}{{a}_{8}}$ | B. | $\frac{{S}_{9}}{{a}_{9}}$ | C. | $\frac{{S}_{10}}{{a}_{10}}$ | D. | $\frac{{S}_{11}}{{a}_{11}}$ |
15.设0<b<a<1,则下列不等式不成立的是( )
| A. | 2b<2a<2 | B. | $0<{log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}$b | ||
| C. | ab<b2<1 | D. | ab<a2<1 |
5.若二项式(x2-$\frac{2}{x}$)n 的展开式中的二项式系数和为64,则展开式中的常数项为( )
| A. | -240 | B. | -160 | C. | 160 | D. | 240 |
12.若函数f(x)=|ax+x2-xlna-m|-3(a>0且a≠1)有两个零点,则m的取值范围( )
| A. | (-2,4) | B. | (-4,2) | C. | (-1,3) | D. | (-3,1) |