如图是一个空间几何体的三视图.则该几何体的表面积是( )A．16+πB．4πC．24+πD．24 题目和参考答案——青夏教育精英家教网—

题目内容

14．如图是一个空间几何体的三视图，则该几何体的表面积是（　　）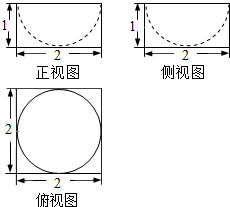

A．

16+π

B．

4π

C．

24+π

D．

分析根据三视图给出的数据可判断：
底面边长为2的正方形，高位1的四棱柱，棱柱内有一个半球，球半径为1，
根据几何体的性质，转化为正方形，矩形，圆的面积求解．

解答解：根据三视图给出的数据可判断：
底面边长为2的正方形，高位1的四棱柱，棱柱内有一个半球，球半径为1，
所以该几何体的表面积2²+4×2×1$+\frac{1}{2}×4×π×{1}^{2}$+（4-π×1²）=16+π．
故选：A．

点评本题考查了空间几何体，组合体的三视图的运用，关键是判断组合体的构成，运用数据求解面积，难度不大，需要计算准确．

练习册系列答案

金榜一号同步单元全程达标测试AB卷系列答案

18．已知x∈（-$\frac{π}{2}$，0）且cosx=$\frac{\sqrt{3}}{2}$，则tan2x=（　　）

A．

$\sqrt{3}$

B．

-$\frac{\sqrt{3}}{3}$

2．

如图，多面体ABCD-A₁E中，底面ABCD为正方形，AA₁⊥平面ABCD，CE⊥平面ABCD，AA₁=2AB=4，且CE=λAA₁，A₁C⊥平面BED．
（1）求λ的值；
（2）求二面角A₁-BD-E的余弦值．

9．若a＞0，b＞0，且ab+a+2b=30，试求ab的最大值及a+2b的最小值．

19．设二元一次不等式组$\left\{\begin{array}{l}x+2y-19≥0\\ \;x-y+8≥0\\ 2x+y-14≤0\end{array}\right.$所表示的平面区域为M，若函数y=a^x（a＞0，且a≠1）的图象经过区域M，则实数a的取值范围为[2，9]．

6．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}+\overrightarrow{b}$=（$\sqrt{3}$，1），求：
（1）|$\overrightarrow{a}-\overrightarrow{b}$|；
（2）$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角．

3．在△ABC中，若∠A=60°，a=1，求△ABC内切圆半径R的最大值．

4．下列函数中，既是奇函数，又在（-∞，+∞）上为增函数的是（　　）

试题分类