题目内容
3.在△ABC中,若∠A=60°,a=1,求△ABC内切圆半径R的最大值.分析 当A在$\widehat{AB}$的中点时,A距离BC最远,△ABC内切圆半径R的最大,根据圆的性质可知当△ABC内切圆半径R的最大时,△ABC为正三角形,进而可求满足条件的内切圆半径
解答 解:当A在$\widehat{AB}$的中点时,A距离BC最远,△ABC内切圆半径R的最大,
设△ABC外接圆半径r,外接圆的圆心O,内切圆的圆心M,
连接AO交BC于点D,
∵A在$\widehat{AB}$的中点且O为三角形的外心,
∴AD⊥BC,BD=DC=$\frac{1}{2}$,AB=AC,
∵A=60°,
∴△ABC为正三角形,
∴M在AD上,且AD=$\frac{\sqrt{3}}{2}$,
设AB与⊙M切于E,连接EM,则EM=EMD=R,
∵∠A=60°,
∴∠BAD=30°,
Rt△AEM中,AM=2EM=2R,
∵AM+MD=AD∴2R+R=$\frac{\sqrt{3}}{2}$,
∴R=$\frac{\sqrt{3}}{6}$,即R的最大值为$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$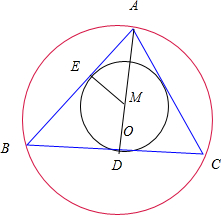
点评 本题主要考查了三角形的内切圆的性质,理解内心的含义是求解本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6. 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
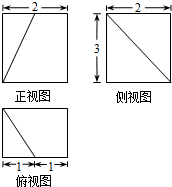
14.如图是一个空间几何体的三视图,则该几何体的表面积是( )


| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
8.实数x,y满足$\left\{\begin{array}{l}{y≥1}\\{y-2x+1≤0}\\{x+y-8≤0}\end{array}\right.$,则z=x-y的最小值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2作平行于C的渐近线的直线交C于点P.若PF1⊥PF2,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |