题目内容
18.已知x∈(-$\frac{π}{2}$,0)且cosx=$\frac{\sqrt{3}}{2}$,则tan2x=( )| A. | $\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
分析 由条件利用同角三角函数的基本关系,求得 tanx的值,再利用二倍角的正切公式求得 tan2x的值.
解答 解:∵x∈(-$\frac{π}{2}$,0)且cosx=$\frac{\sqrt{3}}{2}$,∴sinx=-$\sqrt{{1-cos}^{2}x}$=-$\frac{1}{2}$,tanx=$\frac{sinx}{cosx}$=-$\frac{\sqrt{3}}{3}$,
则tan2x=$\frac{2tanx}{1{-tan}^{2}x}$=-$\sqrt{3}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系,二倍角的正切公式,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
8.已知不等式组$\left\{\begin{array}{l}{x≤2}\\{y≥1}\\{x-y≥0}\end{array}\right.$的解集记为D,则对?(x,y)∈D使得2x-y取最大值时的最优解是( )
| A. | (2,1) | B. | (2,2) | C. | 3 | D. | 4 |
6. 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
10.已知y=f(x)是定义域为R的单调函数,且x1≠x2,λ≠-1,α=$\frac{{{x_1}+λ{x_2}}}{1+λ},β=\frac{{{x_2}+λ{x_1}}}{1+λ}$,若|f(x1)-f(x2)|<|f(α)-f(β)|,则( )
| A. | λ<0 | B. | λ=0 | C. | 0<λ<1 | D. | λ>1 |
14.如图是一个空间几何体的三视图,则该几何体的表面积是( )
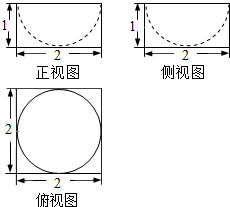

| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2. 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证: