题目内容
19.设二元一次不等式组$\left\{\begin{array}{l}x+2y-19≥0\\ \;x-y+8≥0\\ 2x+y-14≤0\end{array}\right.$所表示的平面区域为M,若函数y=ax(a>0,且a≠1)的图象经过区域M,则实数a的取值范围为[2,9].分析 先依据不等式组$\left\{\begin{array}{l}x+2y-19≥0\\ \;x-y+8≥0\\ 2x+y-14≤0\end{array}\right.$,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用函数y=ax(a>0,a≠1)的图象特征,结合区域的角上的点即可解决问题
解答 解:平面区域M如如图所示.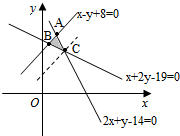
求得A(2,10),C(3,8),B(1,9).
由图可知,欲满足条件必有a>1且图象在过B、C两点的图象之间.
当图象过B点时,a1=9,
∴a=9.
当图象过C点时,a3=8,
∴a=2.
故a的取值范围为[2,9].
点评 本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础.

练习册系列答案
相关题目
2.复数$\frac{(1+i)^{2}}{1-i}$=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
14.如图是一个空间几何体的三视图,则该几何体的表面积是( )


| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |