题目内容
17.设x,y满足约束条件$\left\{\begin{array}{l}{1≤x≤3}\\{-1≤x-y≤0}\end{array}\right.$,则z=2x-y的最大值为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.
解答 解:作出不等式组对应的平面区域如图:(阴影部分ABCD).
由z=2x-y得y=2x-z,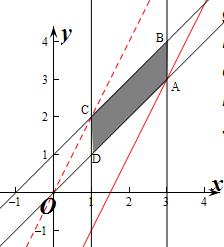
平移直线y=2x-z,
由图象可知当直线y=2x-z经过点A时,直线y=2x-z的截距最小,
此时z最大.
由$\left\{\begin{array}{l}{x=3}\\{x-y=0}\end{array}\right.$,解$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,即A(3,3)
将A(3,3)的坐标代入目标函数z=2x-y,
得z=6-3=3.即z=2x-y的最大值为3.
故选:A
点评 本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\left\{\begin{array}{l}cos\frac{πx}{6},0<x≤8\\ lo{g}_{2}x,x>8\end{array}\right.$,则f(f(-16))=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.已知不等式组$\left\{\begin{array}{l}{x≤2}\\{y≥1}\\{x-y≥0}\end{array}\right.$的解集记为D,则对?(x,y)∈D使得2x-y取最大值时的最优解是( )
| A. | (2,1) | B. | (2,2) | C. | 3 | D. | 4 |
5.已知集合M={x|x2-4x>0},N={x|m<x<8},若M∩N={x|6<x<n},则m+n=( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
2.复数$\frac{(1+i)^{2}}{1-i}$=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
6. 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
14.如图是一个空间几何体的三视图,则该几何体的表面积是( )
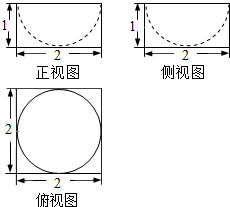

| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.