题目内容
6.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}+\overrightarrow{b}$=($\sqrt{3}$,1),求:(1)|$\overrightarrow{a}-\overrightarrow{b}$|;
(2)$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角.
分析 (1)由已知,得到两个向量的数量积,然后将所求平方可求;
(2)利用数量积公式求之.
解答 解:(1)由已知$\overrightarrow{a}+\overrightarrow{b}$=($\sqrt{3}$,1),所以($\overrightarrow{a}+\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}•\overrightarrow{b}$=4,所以$\overrightarrow{a}•\overrightarrow{b}$=0,
所以|$\overrightarrow{a}-\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}•\overrightarrow{b}$=4,所以|$\overrightarrow{a}-\overrightarrow{b}$|=2;
(2)$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角的余弦值为$\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}||\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{2×2}=\frac{1-3}{4}=-\frac{1}{2}$,
所以$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角为120°.
点评 本题考查了向量的模的求法以及利用数量积公式求向量的夹角;属于基础题.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | λ<0 | B. | λ=0 | C. | 0<λ<1 | D. | λ>1 |

| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
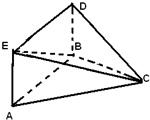 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.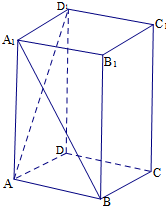
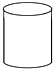
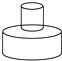
 用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?
用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?