题目内容
9.若a>0,b>0,且ab+a+2b=30,试求ab的最大值及a+2b的最小值.分析 由a>0,b>0,运用基本不等式可得ab+a+2b=30≥ab+2$\sqrt{2ab}$,令$\sqrt{ab}$=t(t>0),得到二次不等式,解得t的范围,即可得到ab的最大值和a+2b的最小值.
解答 解:由a>0,b>0,
则ab+a+2b=30≥ab+2$\sqrt{2ab}$,
令$\sqrt{ab}$=t(t>0),
则t2+2$\sqrt{2}$t-30≤0,
解得0<t≤3$\sqrt{2}$,
即有ab≤18,
则30-(a+2b)≤18,
a+2b≥12,
当且仅当a=2b=6时,
ab的最大值为18,a+2b的最小值为12.
点评 本题考查基本不等式的运用:求最值,同时考查二次不等式的解法,注意最值取得的条件,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
10.已知y=f(x)是定义域为R的单调函数,且x1≠x2,λ≠-1,α=$\frac{{{x_1}+λ{x_2}}}{1+λ},β=\frac{{{x_2}+λ{x_1}}}{1+λ}$,若|f(x1)-f(x2)|<|f(α)-f(β)|,则( )
| A. | λ<0 | B. | λ=0 | C. | 0<λ<1 | D. | λ>1 |
14.如图是一个空间几何体的三视图,则该几何体的表面积是( )
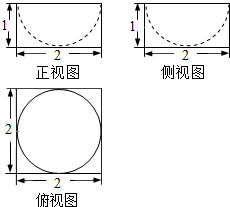

| A. | 16+π | B. | 4π | C. | 24+π | D. | 24 |
19.阅读如图所示的程序框图,运行相应的程序,若输入x的值为-5,则输出y的值为( )

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证: