题目内容
10.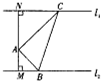 如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.
如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.
分析 根据已知条件把原式转化为sin∠MBA+sin∠NCA,进而利用角的关系,和两角和公式对其化简确定最大值.
解答 解:∵AM=1,AN=$\sqrt{3}$.
∴$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$=$\frac{AM}{AB}$+$\frac{AN}{AC}$=sin∠MBA+sin∠NCA,
∵∠MAB+∠NAC=90°,∠NCA+∠NAC=90°,
∴∠NAC=∠MAB,
∴∠MAB+∠MBA=90°,
∴sin∠MBA+sin∠NCA=sin∠MBA+cos∠MBA=$\sqrt{2}$sin(∠MBA+$\frac{π}{4}$)≤$\sqrt{2}$,当∠MBA=$\frac{π}{4}$取最大值,
故答案为:$\sqrt{2}$
点评 本题主要考查了解三角形问题的实际应用.解题重要的地方是把实际问题转化为解三角形的问题.

练习册系列答案
相关题目
18.已知△ABC是半径为5的圆O的内接三角形,且$tanA=\frac{4}{3}$,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+y的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | $\frac{5}{8}$ |
2.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围为( )
| A. | (-∞,0] | B. | [-1,3] | C. | [3,5] | D. | [5,7] |
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.