题目内容
4.设函数f(x)=2x-$\frac{3}{x}$+alnx(a∈R),g(x)=3x-$\frac{3}{x}$.(1)求函数f(x)的单调区间;
(2)若函数g(x)的图象与f(x)的图象有两个交点,求实数a的取值范围.
分析 (1)先求导,根据△与0的关系进行分类讨论,利用导数和函数的单调性的关系即可求出单调区间;
(2)化简f(x)-g(x)=0,得到alnx=x,分别画出分别画出y=x和y=alnx的图象,先求出当直线y=x和曲线y=alnx相切时a的值,观察即可得到函数g(x)的图象与f(x)的图象有两个交点的a的取值范围.
解答 解:(1)∵f(x)=2x-$\frac{3}{x}$+alnx(a∈R),x>0,
∴f′(x)=2+$\frac{3}{{x}^{2}}$+$\frac{a}{x}$=$\frac{2{x}^{2}+ax+3}{{x}^{2}}$,x>0,
当△=a2-24≤0时,即-2$\sqrt{6}$≤a≤2$\sqrt{6}$,2x2+ax+3≥0恒成立,
∴f′(x)≥0恒成立,
∴f(x)在(0,+∞)上单调递增,
当△=a2-24>0时,即a<-2$\sqrt{6}$,或a>2$\sqrt{6}$时,
令f′(x)=0,解得x1=$\frac{-a-\sqrt{{a}^{2}-24}}{4}$,x2=$\frac{-a+\sqrt{{a}^{2}-24}}{4}$,
若a>2$\sqrt{6}$时,则x1<x2<0,f(x)在(0,+∞)上单调递增,
若a<-2$\sqrt{6}$,则0<x1<x2,
当f′(x)>0时,即x>x2,或x<x1,函数单调递增,
当f′(x)<0时,即x1<x<x2,函数单调递减,
综上所述,当a≥-2$\sqrt{6}$时,函数f(x)在(0,+∞)上单调递增,
当a<-2$\sqrt{6}$时,函数f(x)在(0,$\frac{-a-\sqrt{{a}^{2}-24}}{4}$)和($\frac{-a+\sqrt{{a}^{2}-24}}{4}$,+∞)上单调递增,在($\frac{-a-\sqrt{{a}^{2}-24}}{4}$,$\frac{-a+\sqrt{{a}^{2}-24}}{4}$)单调递减;
(2)∵设h(x)=f(x)-g(x)=alnx-x=0(a∈R),
分别画出y=x和y=alnx的图象,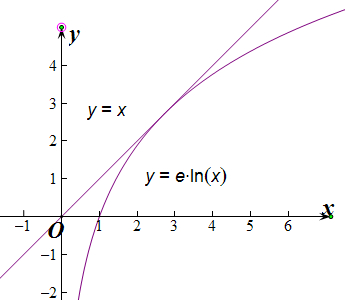
当直线y=x和曲线y=alnx相切时,设切点为(x0,x0),
∴y′=$\frac{a}{x}$
∴$\frac{a}{{x}_{0}}$=1,
即x0=a,
∴a=alma,
解得a=e,
∵函数g(x)的图象与f(x)的图象有两个交点
∴a>e,
故a的取值范围为(e,+∞).
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查学生分析解决问题的能力,属于中档题

 阅读快车系列答案
阅读快车系列答案| A. | 5 | B. | 25 | C. | -25 | D. | -5或5 |
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
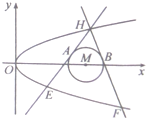 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.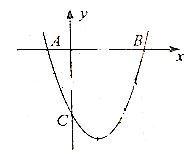 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.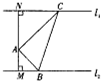 如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.
如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.