��Ŀ����
20����֪����C�ļ����귽���Ǧ�=4cos�ȣ��Լ���Ϊƽ��ֱ������ϵ��ԭ�㣬����Ϊx��������ᣬ����ƽ��ֱ������ϵ��ֱ��l�IJ���������$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+1}\\{y=\frac{1}{2}t}\end{array}\right.$��tΪ����������1��������C��ֱ�����귽�̺�ֱ��l����ͨ���̣�
��2����֪��P��1��0������ֱ��l������C����A��B���㣬��|PA|•|PB|��ֵ��
���� ��1���ѵ�ʽ��=4cos������ͬʱ���Ԧѣ�����x=��cos�ȣ���2=x2+y2�ô𰸣�ֱ����ֱ�ߵIJ���������ȥ����t�õ�ֱ�ߵ���ͨ���̣�
��2����ֱ�ߵIJ������̴���Բ����ͨ���̣�����ֱ�߲��������в���t�ļ����������|PA|•|PB|��ֵ��
��� �⣺��1���ɦ�=4cos�ȣ��æ�2=4��cos�ȣ���x2+y2-4x=0��
��$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+1}\\{y=\frac{1}{2}t}\end{array}\right.$����t=2y������$x=\frac{\sqrt{3}}{2}t+1$���ã�$y=\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}$��
��2����$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+1}\\{y=\frac{1}{2}t}\end{array}\right.$����x2+y2-4x=0����${t}^{2}-\sqrt{3}t-3=0$��
��|PA|•|PB|=|t1t2|=3��
���� ���⿼��������̻���ͨ���̣����鼫���귽�̻�ֱ�����귽�̣�������ֱ�ߵIJ��������в���t�ļ������壬�ǻ����⣮

��ϰ��ϵ�д�
�����Ŀ
15����֪����f��x��=$\frac{sinx}{|cosx|}$������f��x������С�������ǣ�������
| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{2}$ | C�� | �� | D�� | 2�� |
5����֪xy=1����O��y��$\frac{1}{2}$����$\frac{{x}^{2}+16{y}^{2}}{x-4y}$����СֵΪ��������
| A�� | 2$\sqrt{2}$ | B�� | $\frac{17}{3}$ | C�� | 4$\sqrt{2}$ | D�� | 4 |
12����֪��P��x��y��������$\left\{\begin{array}{l}x=-2+cos��\\ y=sin��\end{array}\right.$����Ϊ�������Ҧȡ�[�У�2�У����ϣ����P��ֱ��$\left\{\begin{array}{l}x=2+t\\ y=-1-t\end{array}\right.��t$Ϊ�������ľ����ȡֵ��Χ�ǣ�������
| A�� | [-$\frac{{3\sqrt{2}}}{2}$��$\frac{{3\sqrt{2}}}{2}$] | B�� | [$\frac{{3\sqrt{2}}}{2}$-1��$\frac{{3\sqrt{2}}}{2}$+1] | C�� | ��$\sqrt{2}$��2$\sqrt{2}$] | D�� | ��$\sqrt{2}$��$\frac{{3\sqrt{2}}}{2}$+1] |
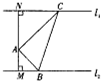 ��ͼ��A������ƽ��ֱ��֮���һ���㣬�ҵ�A������ƽ��ֱ�ߵľ���ֱ�ΪAM=1��AN=$\sqrt{3}$�����ABC��AC��AB���Ҷ���B��C�ֱ�������ƽ��ֱ�����˶�����$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$�����ֵΪ$\sqrt{2}$��
��ͼ��A������ƽ��ֱ��֮���һ���㣬�ҵ�A������ƽ��ֱ�ߵľ���ֱ�ΪAM=1��AN=$\sqrt{3}$�����ABC��AC��AB���Ҷ���B��C�ֱ�������ƽ��ֱ�����˶�����$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$�����ֵΪ$\sqrt{2}$��