题目内容
设函数f(x)的定义域关于原点对称且满足:
(i)f(x1-x2)=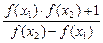 ;
;
(ii)存在正常数a使f(a)=1 求证:
求证:
(1)f(x)是奇函数.
(2)f(x)是周期函数,且有一个周期是4.
(i)f(x1-x2)=
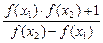 ;
;(ii)存在正常数a使f(a)=1
 求证:
求证: (1)f(x)是奇函数.
(2)f(x)是周期函数,且有一个周期是4.
证明略
(1)不妨令x=x1-x2,
则f(-x)=f(x2-x1)=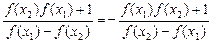
=-f(x1-x2)=-f(x)
∴f(x)是奇函数.
(2)要证f(x+4a)=f(x),可先计算f(x+a),f(x+2a).
∵f(x+a)=f[x-(-a)]=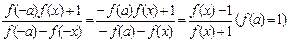

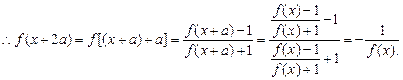
∴f(x+4a)=f[(x+2a)+2a]=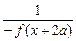 =f(x),
=f(x),
故f(x)是以4a为周期的周期函数.
则f(-x)=f(x2-x1)=
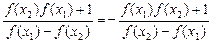
=-f(x1-x2)=-f(x)

∴f(x)是奇函数.
(2)要证f(x+4a)=f(x),可先计算f(x+a),f(x+2a).
∵f(x+a)=f[x-(-a)]=
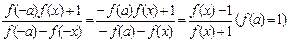

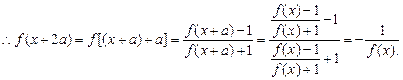
∴f(x+4a)=f[(x+2a)+2a]=
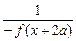 =f(x),
=f(x),故f(x)是以4a为周期的周期函数.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
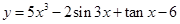 的图象的对称中心是
的图象的对称中心是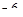 ,0)
,0)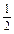 x,求使f(x)=-
x,求使f(x)=-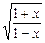 ;
;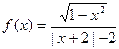 ;(4)
;(4)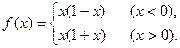
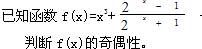
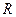 的函数
的函数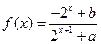 是奇函数。
是奇函数。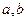 的值;
的值;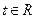 ,不等式
,不等式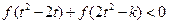 恒成立,求
恒成立,求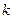 的取值范围;
的取值范围;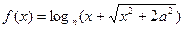 是奇函数,则a= .
是奇函数,则a= .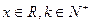 ,定义
,定义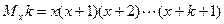 ,例
,例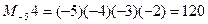 ,则函数
,则函数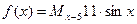 是( )
是( )