题目内容
【题目】【2017届广西陆川县中学高三文上学期二模】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证: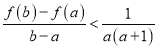 .
.
【答案】(I)当![]() 时,
时,![]() 在
在![]() 上单调递增,无单调递减区间,当
上单调递增,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】
试题分析:(I)利用![]() 时
时![]() 为单调增函数,
为单调增函数,![]() 时
时![]() 为单调减函数这一性质来分情况讨论题中
为单调减函数这一性质来分情况讨论题中![]() 单调区间问题;(II)根据函数单调性与最值,若
单调区间问题;(II)根据函数单调性与最值,若![]() 在
在![]() 上恒成立,则函数的最大值小于或等于零.当
上恒成立,则函数的最大值小于或等于零.当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,说明
,说明![]() 时
时![]() ,不合题意舍去.当
,不合题意舍去.当![]() 时,
时,![]() 的最大值小于零.但
的最大值小于零.但![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 只能等于零.令
只能等于零.令![]() 即可求得答案;(III)首先将
即可求得答案;(III)首先将![]() 的表达式表达出来,化简转化为
的表达式表达出来,化简转化为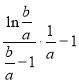 的形式,再根据(II)的结论得到
的形式,再根据(II)的结论得到![]() ,后逐步化简
,后逐步化简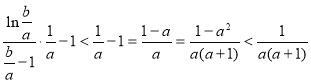 ,原命题得证.
,原命题得证.
试题解析:(I)![]() ,
,
当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上单调递增,无单调递减区间;
上单调递增,无单调递减区间;
当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() ,此时
,此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)由(I)知:当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() ,显然不成立;
,显然不成立;
当![]() 时,
时,![]() ,只需
,只需![]() 即可,
即可,
令![]() ,则
,则![]() ,
,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() .
.
![]() 对
对![]() 恒成立,也就是
恒成立,也就是![]() 对
对![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,![]() 若
若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() .
.
(III)证明: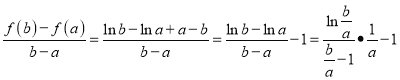 ,
,
由(II)得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又由![]() 得
得![]() ,所以有
,所以有![]() ,即
,即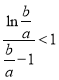 .
.
则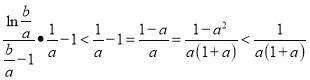 ,
,
则原不等式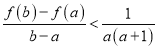 成立.
成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某种商品在![]() 天每件的销售价格
天每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系如下表:
(天)之间的关系如下表:
|
|
|
|
|
|
|
|
|
|

(![]() )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(![]() )根据表
)根据表![]() 提供的数据,写出日销售量
提供的数据,写出日销售量![]() 与时间
与时间![]() 的一次函数关系式.
的一次函数关系式.
(![]() )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天.(日销售金额
天中的第几天.(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)