题目内容
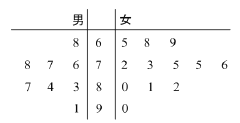
【题目】某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示.成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
(Ⅰ)求出8名男生的平均成绩和12 名女生成绩的中位数;
(Ⅱ)按照获奖类型,用分层抽样的方法从这20名学生中抽取5人,再从选出的5人中任选3人,求恰有1人获“优秀奖”的概率.
【答案】(I)平均数为![]() ,中位数为
,中位数为![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)由平均数及中位数的概念,根据茎叶图可得结果;(Ⅱ)由茎叶图可知,获“纪念奖”的有12人,获“优秀奖”的有8人.用分层抽样的方法从中抽取5人,则“纪念奖”抽取![]() 人,“优秀奖”有2人,利用列举法及古典概型计算公式可求出结果.
人,“优秀奖”有2人,利用列举法及古典概型计算公式可求出结果.
试题解析:
解:(Ⅰ)8名男生的平均成绩为:
![]() .
.
12 名女生成绩的中位数为75.
(Ⅱ)由茎叶图可知,获“纪念奖”的有12人,获“优秀奖”的有8人.用分层抽样的方法从中抽取5人,则“纪念奖”抽取![]() 人,分别记为
人,分别记为![]() ,“优秀奖”有2人,分别记为
,“优秀奖”有2人,分别记为![]() .
.
从这5 人中选取3 人,所有结果有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10个.这些事件的出现是等可能的.
共10个.这些事件的出现是等可能的.
恰有人获“优秀奖”的结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6个.
,共6个.
所以,选出的3人中恰有1人获“优秀奖”的概率![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
【题目】
周销售量(单位:吨) | 2 | 3 | 4 |
频数 | 20 | 50 | 30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,![]() 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.