题目内容
18.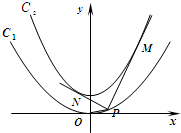 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.(Ⅰ)求抛物线C1的方程及其准线方程;
(Ⅱ)过抛物线C1上的动点P作抛物线C2的两条切线PM、PN,切点为M、N.若PM、PN的斜率乘积为m,且m∈[$\frac{3}{2}$,$\frac{7}{2}$],求|OP|的取值范围.
分析 (Ⅰ)写出C1的焦点为F(0,$\frac{p}{2}$),代入抛物线C2方程即可求得p值,从而可得抛物线C1的方程及其准线方程;
(Ⅱ)任取点P(t,t2),设过点P的C2的切线方程为y-t2=k(x-t).联立切线方程与抛物线C2的方程,消掉y得x的二次方程,由相切得△=0,整理为关于k的二次方程,设PM,PN的斜率分别为k1,k2,由韦达定理可用t表示出m,根据m范围可得t2范围,由两点距离公式可得|OP|的范围.
解答 解:(Ⅰ)C1的焦点为F(0,$\frac{p}{2}$),所以$\frac{p}{2}$=0+$\frac{1}{4}$,p=$\frac{1}{2}$.
故C1的方程为x2=y,其准线方程为y=-$\frac{1}{4}$.…(4分)
(Ⅱ)任取点P(t,t2),设过点P的C2的切线方程为y-t2=k(x-t).…(5分)
代入抛物线方程,得2x2-4kx+4tk-4t2+1=0.…(6分)
由△=(2k)2-8(4tk-4t2+1)=0,化简得2k2-4tk+4t2-1=0,
记PM,PN的斜率分别为k1,k2,则m=k1k2=2t2-$\frac{1}{2}$,
因为m∈[$\frac{3}{2}$,$\frac{7}{2}$],所以t2∈[1,2]…(10分)
所以|OP|2=t2+t4=(t2+$\frac{1}{2}$)2-$\frac{1}{4}$∈[2,6],
所以|OP|∈[$\sqrt{2}$,$\sqrt{6}$].…(12分)
点评 本题考查抛物线方程、直线方程及直线与抛物线的位置关系,本题中P点坐标设法运用了抛物线的参数方程,简化了运算,给解决问题提供了方便.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.现有3名老师,8名男生和5名女生共16人,若需1名老师和1名学生参加,则不同的选法种数为( )
| A. | 39种 | B. | 24种 | C. | 15种 | D. | 16种 |
13.要证:a2+b2-1-a2b2≤0,只要证明( )
| A. | 2ab-1-a2b2≤0 | B. | ${a^2}+{b^2}-1-\frac{{{a^4}+{b^4}}}{2}≤0$ | ||
| C. | $\frac{{{{(a+b)}^2}}}{2}-1-{a^2}{b^2}≤0$ | D. | (a2-1)(b2-1)≥0 |
3.函数f(x)=$\frac{\sqrt{2x+1}}{x-3}$的定义域为( )
| A. | {x|x≥-$\frac{1}{2}$} | B. | {x|x>-$\frac{1}{2}$且x≠3} | C. | {x|x≥-$\frac{1}{2}$且x≠3} | D. | {x|x≠3} |
10.设a>0,b>0.若$\sqrt{3}$是3a与3b的等比中项,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\root{4}{3}$ |
8.将编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒中,每个盒中放球的个数不受限制,恰好有一个盒子是空的概率为( )
| A. | $\frac{9}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{16}$ |