题目内容
6.已知$\overrightarrow{a}=(λ,2)\overrightarrow{b}=(-3,5)$,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角,则λ的值是$\frac{10}{3}$.分析 向量夹角为直角,数量积为0 得到所求.
解答 解:因为$\overrightarrow{a}=(λ,2)\overrightarrow{b}=(-3,5)$,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角,
所以-3λ+10=0,解得$λ=\frac{10}{3}$;
故答案为:$\frac{10}{3}$.
点评 本题考查了向量垂直,数量积为0.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设等差数列{an}的前n项和Sn,若a1+a5+a8=a2+12,则S11=( )
| A. | 44 | B. | 66 | C. | 100 | D. | 132 |
17.一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
(1)作出散点图;
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产缺损零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
1.已知在函数f(x)=ex2+aex图象上点(1,f(1))处切线的斜率为e,则${∫}_{0}^{1}$f(x)dx=( )
| A. | 1-$\frac{2}{3}$ e | B. | 1+$\frac{2}{3}$e | C. | $\frac{2}{3}$e | D. | 1 |
15.若集合P={y|y=$\sqrt{x}$,x≥0},P∩Q=Q,则集合Q不可能是( )
| A. | ∅ | B. | {y|y=x2} | C. | {y|y=2x} | D. | {y|y=lgx} |
16.若角α的终边经过点$A\;(\frac{3}{5},\;\frac{4}{5})$,则sinα=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
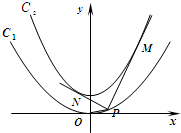 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.