题目内容
13.要证:a2+b2-1-a2b2≤0,只要证明( )| A. | 2ab-1-a2b2≤0 | B. | ${a^2}+{b^2}-1-\frac{{{a^4}+{b^4}}}{2}≤0$ | ||
| C. | $\frac{{{{(a+b)}^2}}}{2}-1-{a^2}{b^2}≤0$ | D. | (a2-1)(b2-1)≥0 |
分析 将左边因式分解,即可得出结论.
解答 解:要证:a2+b2-1-a2b2≤0,只要证明(a2-1)(1-b2)≤0,
只要证明(a2-1)(b2-1)≥0.
故选:D.
点评 综合法(由因导果)证明不等式、分析法(执果索因)证明不等式.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
3.等差数列{an}中,a1+a2=3,a3+a4=7,则a5+a6=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
4.已知向量$\vec a$=(1,2),$\vec b$=(k+1,3),若$\vec a$与$\vec b$的夹角为锐角,则实数k的取值范围为( )
| A. | (-7,+∞) | B. | (-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) | C. | [-7,+∞) | D. | [-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) |
1.已知在函数f(x)=ex2+aex图象上点(1,f(1))处切线的斜率为e,则${∫}_{0}^{1}$f(x)dx=( )
| A. | 1-$\frac{2}{3}$ e | B. | 1+$\frac{2}{3}$e | C. | $\frac{2}{3}$e | D. | 1 |
2.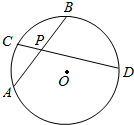 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )| A. | 7 | B. | $\sqrt{39}$ | C. | $\sqrt{7}$ | D. | 8 |
3.已知直线x-$\sqrt{3}$y-1=0与圆C:(x-1)2+(y-2)2=4交于A,B两点,则弦AB的长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
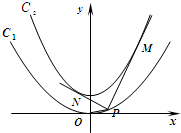 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.