题目内容
3.函数f(x)=$\frac{\sqrt{2x+1}}{x-3}$的定义域为( )| A. | {x|x≥-$\frac{1}{2}$} | B. | {x|x>-$\frac{1}{2}$且x≠3} | C. | {x|x≥-$\frac{1}{2}$且x≠3} | D. | {x|x≠3} |
分析 根据函数的解析式列出不等式组,求出解集可得函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{2x+1≥0}\\{x-3≠0}\end{array}\right.$,解得x$≥-\frac{1}{2}$且x≠3,
所以函数的定义域是{x|x≥-$\frac{1}{2}$且x≠3},
故选:C.
点评 本题考查了函数的定义域的求法,掌握求函数定义域的法则是解题的关键,属于基础题.

练习册系列答案
相关题目
15.若集合P={y|y=$\sqrt{x}$,x≥0},P∩Q=Q,则集合Q不可能是( )
| A. | ∅ | B. | {y|y=x2} | C. | {y|y=2x} | D. | {y|y=lgx} |
12.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别是F1,F2,过F2作直线PF2⊥F1F2,交双曲线C于P,若△PF1F2为等腰直角三角形,则双曲线C的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$+2 |
13.向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(n,-1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则mn=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
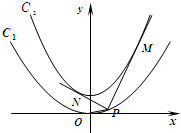 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.