题目内容
7.已知甲、乙两个圆柱的底面积分别为S1,S2,且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{9}{4}$,体积分别为V1,V2,若它们的侧面积相等,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.分析 设出两个圆柱的底面半径与高,通过侧面积相等,推出高的比,然后求解体积的比.
解答 解:设两个圆柱的底面半径分别为R,r;高分别为H,h;
∵$\frac{{S}_{1}}{{S}_{2}}$=$\frac{9}{4}$,
∴$\frac{R}{r}$=$\frac{3}{2}$,
∵它们的侧面积相等,$\frac{2πRH}{2πrh}$=1
∴$\frac{H}{h}$=$\frac{2}{3}$,
∴$\frac{V_1}{V_2}$=$\frac{π{R}^{2}H}{π{r}^{2}h}$=($\frac{3}{2}$)2•$\frac{2}{3}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查柱体体积公式以及侧面积公式的直接应用,是基础题目.

练习册系列答案
相关题目
17.一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
(1)作出散点图;
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产缺损零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
15.若集合P={y|y=$\sqrt{x}$,x≥0},P∩Q=Q,则集合Q不可能是( )
| A. | ∅ | B. | {y|y=x2} | C. | {y|y=2x} | D. | {y|y=lgx} |
2.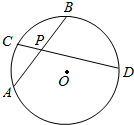 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )| A. | 7 | B. | $\sqrt{39}$ | C. | $\sqrt{7}$ | D. | 8 |
12.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别是F1,F2,过F2作直线PF2⊥F1F2,交双曲线C于P,若△PF1F2为等腰直角三角形,则双曲线C的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$+2 |
19.用样本频率分布估计总体频率分布的过程中,下列说法正确的是( )
| A. | 总体容量越大,估计越精确 | B. | 总体容量越小,估计越精确 | ||
| C. | 样本容量越大,估计越精确 | D. | 样本容量越小,估计越精确 |
16.若角α的终边经过点$A\;(\frac{3}{5},\;\frac{4}{5})$,则sinα=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
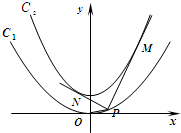 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.