题目内容
8.已知一个圆柱的侧面积是2π,体积为π,则其全面积是4π.分析 利用圆柱的侧面积是2π,体积为π,求出r,h,即可求出其全面积.
解答 解:侧面积:2πrh=2π 得rh=1
体积:πr2h=π,得r2h=1,
公式联立得r=1,h=1
则全面积=侧面积+上下圆面积=2π+2πr2=4π.
故答案为:4π.
点评 本题考查圆柱的侧面积、体积、全面积,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
18.函数y=$\frac{1}{{\sqrt{{{log}_{\frac{1}{2}}}(4x-3)}}}$的定义域为( )
| A. | .(1,+∞) | B. | ($\frac{3}{4}$,∞) | C. | ( $\frac{3}{4}$,1) | D. | .( $\frac{3}{4}$,1)∪(1,+∞) |
16.设等差数列{an}的前n项和Sn,若a1+a5+a8=a2+12,则S11=( )
| A. | 44 | B. | 66 | C. | 100 | D. | 132 |
3.等差数列{an}中,a1+a2=3,a3+a4=7,则a5+a6=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
17.一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
(1)作出散点图;
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产缺损零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
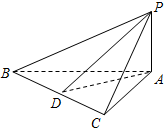 如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.
如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.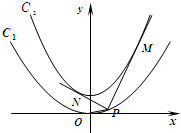 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.