题目内容
8.将编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒中,每个盒中放球的个数不受限制,恰好有一个盒子是空的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{16}$ |
分析 利用先分组,后排列的方法求恰好有一个盒子空的放法种数,再求出编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒中的放法种数,代入古典概型概率公式计算.
解答 解:先把四个分成3组,共有C42=6种方法;
把3组小球放入编号为A、B、C、D的四个盒子中的3个,有A43=24种放法,
∴编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒中,每个盒中放球的个数不受限制,恰好有一个盒子是空的放法有24×6=144种方法;
4编号为1、2、3、4的四个小球任意地放入A、B、C、D四个小盒有44=256种放法,
∴恰好有一个盒子空的概率为$\frac{144}{256}$=$\frac{9}{16}$,
故选:A.
点评 本题考查了古典概型的概率计算,考查了排列组合的应用,本题采用了先分组,后排列的方法求恰好有一个盒子空的放法种数,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.用样本频率分布估计总体频率分布的过程中,下列说法正确的是( )
| A. | 总体容量越大,估计越精确 | B. | 总体容量越小,估计越精确 | ||
| C. | 样本容量越大,估计越精确 | D. | 样本容量越小,估计越精确 |
16.若角α的终边经过点$A\;(\frac{3}{5},\;\frac{4}{5})$,则sinα=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
3.已知直线x-$\sqrt{3}$y-1=0与圆C:(x-1)2+(y-2)2=4交于A,B两点,则弦AB的长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
13.向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(n,-1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则mn=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
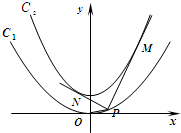 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.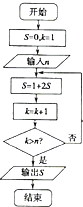 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )