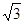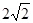题目内容
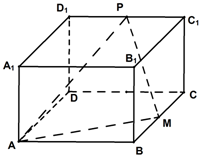
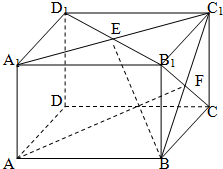
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
(Ⅰ)求证:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.
(Ⅲ)若二面角A-B1E-A1的大小为30°,求AB的长.

(Ⅰ)求证:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.
(Ⅲ)若二面角A-B1E-A1的大小为30°,求AB的长.

(I)以A为原点,
,
,
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,如图,
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E(
,1,0),B1(a,0,1)
故
=(0,1,1),
=(-
,1,-1),
=(a,0,1),
=(
,1,0),
∵
•
=1-1=0
∴B1E⊥AD1;
(II)假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE.此时
=(0,-1,t).
又设平面B1AE的法向量
=(x,y,z).
∵
⊥平面B1AE,∴
⊥B1A,
⊥AE,得
,取x=1,得平面B1AE的一个法向量
=(1,-
,-a).
要使DP∥平面B1AE,只要
⊥
,即有
•
=0,有此得
-at=0,解得t=
,即P(0,0,
),
又DP?平面B1AE,
∴存在点P,满足DP∥平面B1AE,此时AP=
(III)连接A1D,B1C,由长方体ABCD-A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
由(I)知,B1E⊥AD1,且B1C∩B1E=B1.
∴AD1⊥平面DCB1A1,
∴AD1是平面B1A1E的一个法向量,此时
=(0,1,1).
设
与
所成的角为θ,则cosθ=
=
∵二面角A-B1E-A1的大小为30°,
∴|cosθ|=cos30°=
即
=
,解得a=2,即AB的长为2

| AB |
| AD |
| AA1 |
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E(
| a |
| 2 |
故
| AD1 |
| B1E |
| a |
| 2 |
| AB1 |
| AE |
| a |
| 2 |
∵
| AD1 |
| B1E |
∴B1E⊥AD1;
(II)假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE.此时
| DP |
又设平面B1AE的法向量
| n |
∵
| n |
| n |
| n |
|
| n |
| a |
| 2 |
要使DP∥平面B1AE,只要
| n |
| DP |
| n |
| DP |
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又DP?平面B1AE,
∴存在点P,满足DP∥平面B1AE,此时AP=
| 1 |
| 2 |
(III)连接A1D,B1C,由长方体ABCD-A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
由(I)知,B1E⊥AD1,且B1C∩B1E=B1.
∴AD1⊥平面DCB1A1,
∴AD1是平面B1A1E的一个法向量,此时
| AD1 |
设
| AD1 |
| n |
| ||||
|
|
-
| ||||||
|
∵二面角A-B1E-A1的大小为30°,
∴|cosθ|=cos30°=
| ||
| 2 |
-
| ||||||
|
| ||
| 2 |


练习册系列答案
相关题目


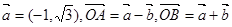 ,若
,若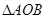 是以
是以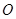 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,