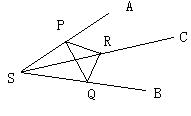
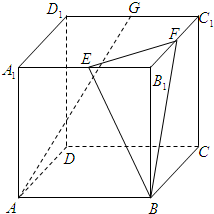
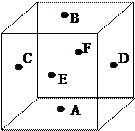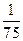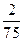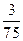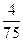题目内容
在如图所示的几何体ABCED中,EC⊥面ABC,DB⊥面ABC,CE=CA=CB=2DB,∠ACB=90°,M为
AD的中点.(1)证明:EM⊥AB;(2)求直线BM和平面ADE所成角的正弦值.
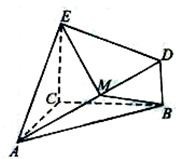
AD的中点.(1)证明:EM⊥AB;(2)求直线BM和平面ADE所成角的正弦值.

(1)证明:以C为原点建立如图所示的空间直角坐标系,设DB=1,则 CE=CA=CB=2.
由于A(2,0,0),B(0,2,0),E(0,0,2),D(0,2,1),M(1,1,
),∴
=(1,1-
),
=(-2,2,0),∴
•
=-2+2+0=0,∴
⊥
,∴EM⊥AB.
(2)由(1)知
=(1,-1,
),
=(-2,2,1),
=(-2,0,2),
=(0,-2,1).
设面ADE的法向量为
=(x,y,z),则
,即
,
取
=(2,1,2)设直线BM和平面ADE所成角为θ,则 sinθ=|cos<
,
>=|
|=
.
由于A(2,0,0),B(0,2,0),E(0,0,2),D(0,2,1),M(1,1,
| 1 |
| 2 |
| EM |
| 3 |
| 2 |
| AB |
| EM |
| AB |
| EM |
| AB |
(2)由(1)知
| BM |
| 1 |
| 2 |
| AD |
| AE |
| DE |
设面ADE的法向量为
| n |
|
|
取
| n |
| BM |
| n |
| ||||
|
|
| 4 |
| 9 |

练习册系列答案
相关题目