题目内容
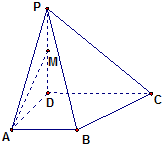
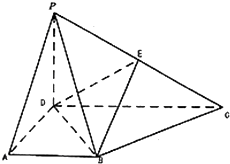
已知四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,AD⊥AB,AD=AB=
CD=1,PD⊥面ABCD,PD=
,E是PC的中点
(1)证明:BE∥面PAD;
(2)求二面角E-BD-C的大小.
| 1 |
| 2 |
| 2 |
(1)证明:BE∥面PAD;
(2)求二面角E-BD-C的大小.

(1)取PD的中点F,连结EF、AF,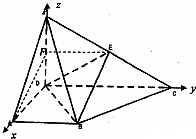
∵E为PC中点,∴EF∥CD,且EF=
CD=1,
在梯形ABCD中,AB∥CD,AB=1,∴EF∥AB,EF=AB,
四边形ABEF为平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,∴BE∥平面PAD.
(2)分别以DA、DB、DP为x、y、z轴,建立空间直角坐标系,如图所示
可得B(1,1,0),C(0,2,0),P(0,0,
),E(0,1,
)
∴
=(1,1,0),
=(-1,0,
)
设
=(x,y,z)为平面BDE的一个法向量,则
取x=1,得y=-1,z=
,
=(1,-1,
)
∵平面ABCD的一个法向量为
=(0,0,1),
∴cos<
,
>=
=
,可得<
,
>=45°
因此,二面角E-BD-C的大小为45°.

∵E为PC中点,∴EF∥CD,且EF=
| 1 |
| 2 |
在梯形ABCD中,AB∥CD,AB=1,∴EF∥AB,EF=AB,
四边形ABEF为平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,∴BE∥平面PAD.
(2)分别以DA、DB、DP为x、y、z轴,建立空间直角坐标系,如图所示
可得B(1,1,0),C(0,2,0),P(0,0,
| 2 |
| ||
| 2 |
∴
| DB |
| BE |
| ||
| 2 |
设
| n |
|
取x=1,得y=-1,z=
| 2 |
| n |
| 2 |
∵平面ABCD的一个法向量为
| m |
∴cos<
| m |
| n |
| ||||
|
| ||
| 2 |
| m |
| n |
因此,二面角E-BD-C的大小为45°.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目