题目内容
(本小题满分12分)数列{an}满足a1=1,an=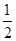 an-1+1 (n≥2)
an-1+1 (n≥2)
⑴ 写出数列{an}的前5项;
⑵ 求数列{an}的通项公式。
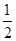 an-1+1 (n≥2)
an-1+1 (n≥2) ⑴ 写出数列{an}的前5项;
⑵ 求数列{an}的通项公式。
⑴ a1="1" ,a2= ⑵ an=2
⑵ an=2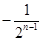 。
。
 ⑵ an=2
⑵ an=2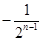 。
。本试题主要是考查了数列递推关系求解数列的通项公式和前n项和。
(1)对于n令值,得到数列的前几项的值。
(2)根据前几项,归纳猜想,得到数列的通项公式,并运用数学归纳法加以证明。
解 ⑴ a1="1" ,a2=
( 猜想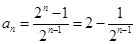
 {an-2}是等比数列 )………4分
{an-2}是等比数列 )………4分
⑵ 解法一由an=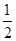 an-1+1 (n≥2) 得an-2=
an-1+1 (n≥2) 得an-2=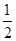 (an-1-2) ………7分
(an-1-2) ………7分
令 bn= an-2 则bn=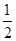 bn-1
bn-1
又b1=a1-2=-1 故{bn}是等比数列,首项-1,公比为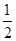 ,………9分
,………9分
bn=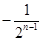 ………11分
………11分
于是 an=2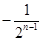 ………12分
………12分
解法二 设 an+k=h(an-1+k)其中k、h为待定系数。
将an=han-1+kh-k 与 an=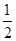 an-1+1 比较得 h=
an-1+1 比较得 h=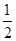 , k=-2
, k=-2
故an-2=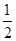 (an-1-2) (n≥2) 而 a1-2=-1
(an-1-2) (n≥2) 而 a1-2=-1
数列{an-2}是以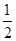 为公比,-1首项的等比数列。
为公比,-1首项的等比数列。
an-2=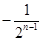 , an=2
, an=2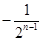 。
。
(1)对于n令值,得到数列的前几项的值。
(2)根据前几项,归纳猜想,得到数列的通项公式,并运用数学归纳法加以证明。
解 ⑴ a1="1" ,a2=

( 猜想
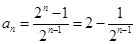
 {an-2}是等比数列 )………4分
{an-2}是等比数列 )………4分⑵ 解法一由an=
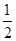 an-1+1 (n≥2) 得an-2=
an-1+1 (n≥2) 得an-2=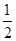 (an-1-2) ………7分
(an-1-2) ………7分令 bn= an-2 则bn=
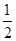 bn-1
bn-1又b1=a1-2=-1 故{bn}是等比数列,首项-1,公比为
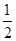 ,………9分
,………9分bn=
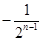 ………11分
………11分于是 an=2
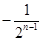 ………12分
………12分解法二 设 an+k=h(an-1+k)其中k、h为待定系数。
将an=han-1+kh-k 与 an=
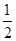 an-1+1 比较得 h=
an-1+1 比较得 h=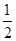 , k=-2
, k=-2故an-2=
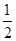 (an-1-2) (n≥2) 而 a1-2=-1
(an-1-2) (n≥2) 而 a1-2=-1数列{an-2}是以
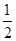 为公比,-1首项的等比数列。
为公比,-1首项的等比数列。an-2=
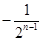 , an=2
, an=2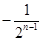 。
。
练习册系列答案
相关题目
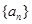 是等比数列,公比
是等比数列,公比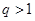 ,前
,前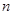 项和为
项和为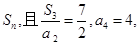
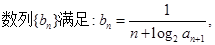
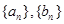 的通项公式;
的通项公式;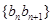 的前
的前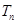 ,求证
,求证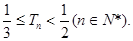
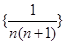 的前
的前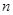 项和为
项和为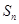 ,则
,则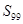 等于
等于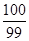
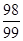
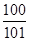
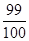
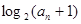 ,{bn}的前n项和为Sn,求证
,{bn}的前n项和为Sn,求证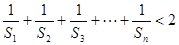
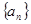 的前n次之和为
的前n次之和为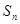 满足
满足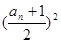
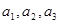 ,
,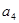 ②猜测数列
②猜测数列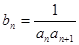 ,数列
,数列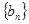 的前n项和为
的前n项和为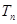 ,求
,求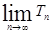 的值.
的值.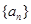 前
前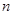 项和为
项和为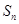 ,若
,若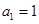 ,
,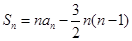 .
.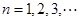
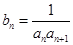 ,数列
,数列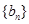 前
前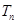 ,证明:
,证明: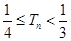 ;
;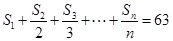 ?若存在,求出
?若存在,求出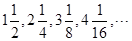 前n项的和为()
前n项的和为()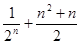
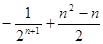
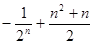
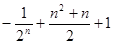
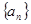 的前
的前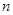 项和
项和 满足
满足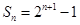 ,则通项公式为 .
,则通项公式为 .