题目内容
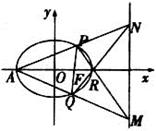
已知椭圆C: (a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
(a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
 (a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
(a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.(Ⅰ)  (Ⅱ) 椭圆的右顶点
(Ⅱ) 椭圆的右顶点
 (Ⅱ) 椭圆的右顶点
(Ⅱ) 椭圆的右顶点(1)由题知抛物线y2 = 16x的准线方程为x =" –" 4,这也是椭圆的左准线方程.设椭圆 的右焦点为F(c,0),其中c =
的右焦点为F(c,0),其中c =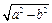 ,则
,则 ,即a2 = 4c.①
,即a2 = 4c.①
由 消去x,得
消去x,得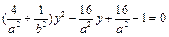 .
.
由于直线x + 2y – 4 = 0与椭圆C相切,所以
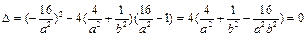 .
.
即4b2 + a2 – 16 = 0,所以4(a2 – c2) + a2 – 16 = 0,
整理得5a2 –4c2 – 16 = 0. ②
将①代入②得5×4c – 4c2 – 16 = 0,即c2 – 5c + 4 = 0,解得c = 1或4.
由于c<a< . 所以c = 1.所以a2 = 4,b2 = 3.所以椭圆C的方程为
. 所以c = 1.所以a2 = 4,b2 = 3.所以椭圆C的方程为 . 5分
. 5分
(2)由(1)知,A(–2,0),F(1,0),椭圆的右准线方程为x = 4.
根据椭圆的对称性,当直线PQ⊥x轴时,四边形MNPQ是等腰梯形,对角线PM、QN的交点在x轴上.此时,直线PQ的方程为x = 1.
由 得
得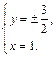 不妨取P(1,
不妨取P(1,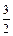 ),Q(1,–
),Q(1,–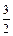 ),
),
故直线AP的方程为y =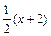 ,将x = 4代入,得N(4,3),
,将x = 4代入,得N(4,3),
所以直线QN的方程为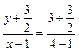 .令y = 0,得x = 2,即直线QN与x轴的交点为R(2,0),
.令y = 0,得x = 2,即直线QN与x轴的交点为R(2,0),
此点恰为椭圆的右顶点.……8分下面只要证明,在一般情况下Q、N、R三点共线即可.
设P(x1,y1),Q(x2,y2),N(4,y3),M(4,y4),直线PQ的方程为x = my + 1.
由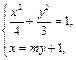 消去x得
消去x得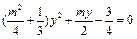 .
.
所以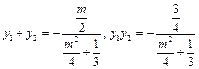 .因为A(–2,0),P(x1,y1),N(4,y3)三点共线,
.因为A(–2,0),P(x1,y1),N(4,y3)三点共线,
所以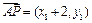 与
与 共线,所以(x1 + 2)y3 = 6y1,即y3 =
共线,所以(x1 + 2)y3 = 6y1,即y3 =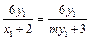 .
.
由于 ,
,
所以 =
=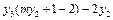
= =
= .
.
所以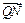 、
、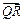 共线,即Q、N、R三点共线.、……12分同理可证,P、M、R三点共线.
共线,即Q、N、R三点共线.、……12分同理可证,P、M、R三点共线.
所以,四边形MNPQ的对角线的交点是定点,此定点恰为椭圆的右顶点.……13分
 的右焦点为F(c,0),其中c =
的右焦点为F(c,0),其中c =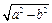 ,则
,则 ,即a2 = 4c.①
,即a2 = 4c.①

由
 消去x,得
消去x,得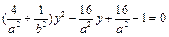 .
.由于直线x + 2y – 4 = 0与椭圆C相切,所以
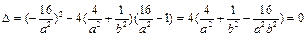 .
.即4b2 + a2 – 16 = 0,所以4(a2 – c2) + a2 – 16 = 0,
整理得5a2 –4c2 – 16 = 0. ②
将①代入②得5×4c – 4c2 – 16 = 0,即c2 – 5c + 4 = 0,解得c = 1或4.
由于c<a<
 . 所以c = 1.所以a2 = 4,b2 = 3.所以椭圆C的方程为
. 所以c = 1.所以a2 = 4,b2 = 3.所以椭圆C的方程为 . 5分
. 5分(2)由(1)知,A(–2,0),F(1,0),椭圆的右准线方程为x = 4.
根据椭圆的对称性,当直线PQ⊥x轴时,四边形MNPQ是等腰梯形,对角线PM、QN的交点在x轴上.此时,直线PQ的方程为x = 1.
由
 得
得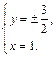 不妨取P(1,
不妨取P(1,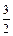 ),Q(1,–
),Q(1,–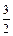 ),
),故直线AP的方程为y =
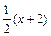 ,将x = 4代入,得N(4,3),
,将x = 4代入,得N(4,3),所以直线QN的方程为
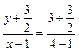 .令y = 0,得x = 2,即直线QN与x轴的交点为R(2,0),
.令y = 0,得x = 2,即直线QN与x轴的交点为R(2,0),此点恰为椭圆的右顶点.……8分下面只要证明,在一般情况下Q、N、R三点共线即可.
设P(x1,y1),Q(x2,y2),N(4,y3),M(4,y4),直线PQ的方程为x = my + 1.
由
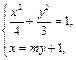 消去x得
消去x得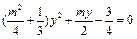 .
.所以
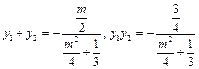 .因为A(–2,0),P(x1,y1),N(4,y3)三点共线,
.因为A(–2,0),P(x1,y1),N(4,y3)三点共线,所以
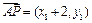 与
与 共线,所以(x1 + 2)y3 = 6y1,即y3 =
共线,所以(x1 + 2)y3 = 6y1,即y3 =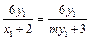 .
.由于
 ,
,所以
 =
=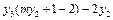
=
 =
= .
.所以
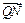 、
、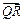 共线,即Q、N、R三点共线.、……12分同理可证,P、M、R三点共线.
共线,即Q、N、R三点共线.、……12分同理可证,P、M、R三点共线.所以,四边形MNPQ的对角线的交点是定点,此定点恰为椭圆的右顶点.……13分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
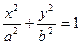 (a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明
(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明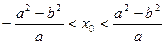 .
.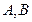 是两个定点,以
是两个定点,以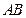 为一条底边作梯形
为一条底边作梯形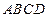 ,使
,使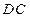 的长为定值,
的长为定值,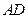 与
与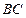 的长之和也是定值,则
的长之和也是定值,则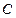 点的轨迹是什么曲线?
点的轨迹是什么曲线?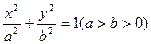 的离心率为
的离心率为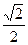 ,若直线
,若直线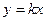 与椭圆的一个交点的横坐标为b,则k的值为( )。
与椭圆的一个交点的横坐标为b,则k的值为( )。


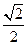
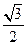
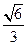
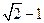
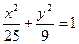 的两个焦点,过F1的直线交椭圆于A、B两点
的两个焦点,过F1的直线交椭圆于A、B两点