题目内容
10．
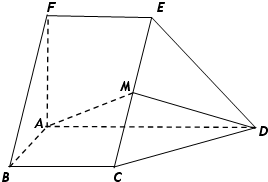如图，在多面体ABCDEF中，FA⊥平面ABCD，BA⊥AD，FE∥AD∥BC，M为CE的中点，EF=FA=AB=BC=$\frac{1}{2}$AD=1．（1）求证：平面AMD⊥平面CDE；
（2）求二面角A-CD-E的余弦值．
分析 （1）取AD中点G，连结CG、GE、GM，通过EC⊥AG、EC⊥MG，以及线面垂直、面面垂直的判定定理即得结论；
（2）取CD中点H，连结GH，则∠EHG即为二面角A-CD-E的平面角，在Rt△EGH中计算即可．
解答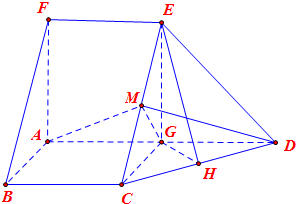 
（1）证明：取AD中点G，连结CG、GE、GM，
由题易知：EC⊥AG，△CEG为等腰直角三角形，
∵M为CE的中点，∴EC⊥MG，
∴EC⊥平面AGM，
∴平面AMD⊥平面CDE；
（2）解：∵EF=FA=AB=BC=$\frac{1}{2}$AD=1，
∴EC=CD=DE=$\sqrt{1+1}$=$\sqrt{2}$，
取CD中点H，连结GH，
则∠EHG即为二面角A-CD-E的平面角，
∵GH=$\frac{CG•DG}{CD}$=$\frac{1×1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$，EH=CE•$sin\frac{π}{3}$=$\sqrt{2}•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2}$，
∴在Rt△EGH中，cos∠EHG=$\frac{GH}{EH}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{3}}{3}$，
即二面角A-CD-E的余弦值为$\frac{\sqrt{3}}{3}$．
点评 本题考查空间中线面平行的判定，考查二面角的三角函数值，注意解题方法的积累，属于中档题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
20．已知Ω是不等式组$\left\{\begin{array}{l}{y≥2}\\{x-y≥1}\\{x+y≤6}\end{array}\right.$所确定的平面区域，记包含区域Ω的半径最小的圆为A，若在圆A内随机取出一点B，则点B在Ω内的概率为（ ）
| A． | -$\frac{1}{π}$ | B． | 1-$\frac{2}{π}$ | C． | $\frac{1}{π}$ | D． | $\frac{2}{π}$ |
1．已知函数f（x）=sin（ωx+φ）的单调增区间为$[kπ-\frac{π}{12}$，kπ+$\frac{5π}{12}]$（k∈Z），则函数f（x）在区间$[0，\frac{π}{2}]$的取值范围是（ ）
| A． | $[-\frac{{\sqrt{3}}}{2}，1]$ | B． | $[-\frac{1}{2}，\frac{{\sqrt{3}}}{2}]$ | C． | $[-\frac{{\sqrt{3}}}{2}，\frac{{\sqrt{3}}}{2}]$ | D． | $[-\frac{1}{2}，1]$ |