题目内容
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,它的顶点构成的四边形面积为4.过点(m,0)作x2+y2=b2的切线l交椭圆C于A、B两点.(1)求椭圆C的方程;
(2)设O为坐标原点,求△OAB面积的最大值.
分析 (1)利用椭圆的离心率定义和菱形的面积公式可得椭圆方程.
(2)根据直线方程和椭圆方程联立方程组,求得弦长,求得三角形的面积,再根据均值不等式求得面积最大值.
解答 解:(1)∵$e=\frac{\sqrt{3}}{2}$∴${e}^{2}=\frac{{c}^{2}}{{a}^{2}}=\frac{3}{4}$.
∴${c}^{2}=\frac{3}{4}{a}^{2}$①
又∵它的顶点构成的四边形面积为4,
∴$\frac{1}{2}\\;ab×4=4$×a×b×4=4,
∴ab=2②
由①②,结合a2-b2=c2,解得a2=4,b2=1,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)(Ⅱ)由题意知,|m|≥1,当m=1时,切线l的方程x=1,
点A、B的坐标分别为($1,\frac{\sqrt{3}}{2}$),($1,-\frac{\sqrt{3}}{2}$)此时$|AB|=\sqrt{3}$;
当m=-1时,同理可得|AB|=$\sqrt{3}$;
当|m|>1时,设切线l的方程为y=k(x-m),
由$\left\{\begin{array}{l}{y=k(x-m)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2-8k2mx+4k2m2-4=0,
设A、B两点的坐标分别为(x1,y1)(x2,y2),
则${x}_{1}+{x}_{2}=\frac{8{k}^{2}m}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{k}^{2}{m}^{2}-4}{1+4{k}^{2}}$,
又由l与圆x2+y2=1相切,得$\frac{|km|}{\sqrt{{k}^{2}+1}}=1$,即m2k2=k2+1,
所以$|AB|=\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$
=$\sqrt{(1+{k}^{2})[\frac{64{k}^{4}{m}^{2}}{(1+4{k}^{2})^{2}}-\frac{4(4{k}^{2}{m}^{2}-4)}{1+4{k}^{2}}]}$=$\frac{4\sqrt{3}|m|}{{m}^{2}+3}$,
由于当m=±3时,|AB|=$\sqrt{3}$
所以,$|AB|=\frac{4\sqrt{3}|m|}{{m}^{2}+3},m∈(-∞,-1]∪[1,+∞)$
因为$|AB|=\frac{4\sqrt{3}|m|}{{m}^{2}+3}=\frac{4\sqrt{3}}{|m|+\frac{3}{|m|}}≤2$且$m=±\sqrt{3}$,此时,|AB|=2,
所以|AB|的最大值为2.
∴S△OAB的最大值为$\frac{1}{2}×2×1=1$
点评 本题主要考查了椭圆方程的求法和直线与椭圆方程的位置关系的应用来求得三角形面积.属难度较大题目,在高考中属压轴题目.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 36 | B. | 45 | C. | 55 | D. | 120 |
| A. | [-3,1] | B. | [-1,3] | C. | [3,+∞) | D. | (-∞,-1] |
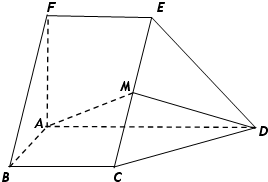 如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1.
如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1.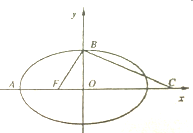 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.