题目内容
1.已知函数f(x)=sin(ωx+φ)的单调增区间为$[kπ-\frac{π}{12}$,kπ+$\frac{5π}{12}]$(k∈Z),则函数f(x)在区间$[0,\frac{π}{2}]$的取值范围是( )| A. | $[-\frac{{\sqrt{3}}}{2},1]$ | B. | $[-\frac{1}{2},\frac{{\sqrt{3}}}{2}]$ | C. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | D. | $[-\frac{1}{2},1]$ |
分析 由条件利用正弦函数的周期性、单调性求出ω、φ的值,再利用正弦函数的定义域和值域求得函数f(x)在区间$[0,\frac{π}{2}]$上的取值范围.
解答 解:由函数f(x)=sin(ωx+φ)的单调增区间为$[kπ-\frac{π}{12}$,kπ+$\frac{5π}{12}]$(k∈Z),可得函数的周期为$\frac{2π}{ω}$=2($\frac{5π}{12}$+$\frac{π}{12}$),求得ω=2.
由2kπ-$\frac{π}{2}$≤2x+φ≤2kπ+$\frac{π}{2}$,k∈z,求得增区间为[kπ-$\frac{π}{4}$-$\frac{φ}{2}$,kπ+$\frac{π}{4}$-$\frac{φ}{2}$],k∈z.
∴-$\frac{π}{12}$=-$\frac{π}{4}$-$\frac{φ}{2}$,且$\frac{5π}{12}$=$\frac{π}{4}$-$\frac{φ}{2}$,求得φ=-$\frac{π}{3}$,故函数f(x)=sin(2x-$\frac{π}{3}$).
在区间$[0,\frac{π}{2}]$上,2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],sin(2x-$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],
故选:A.
点评 本题主要正弦函数的周期性、单调性、定义域和值域,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
9.下列函数中,周期为π,且在$[\frac{π}{4},\frac{π}{2}]$上为减函数的是( )
| A. | $y=cos(x+\frac{5π}{2})$ | B. | $y=cos(2x+\frac{5π}{2})$ | C. | $y=sin(x+\frac{5π}{2})$ | D. | $y=sin(2x+\frac{5π}{2})$ |
13.已知(1+x)n(n∈N*)的展开式中第3项与第8项的二项式系数相等,则这两项的二项式系数为( )
| A. | 36 | B. | 45 | C. | 55 | D. | 120 |
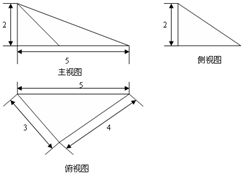
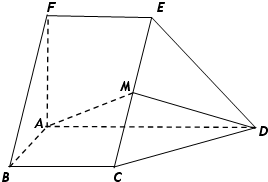 如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1.
如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1.