题目内容
已知平面α⊥平面β,交线为AB,C∈ ,D∈
,D∈ ,
, ,E为BC的中点,AC⊥BD,BD=8.
,E为BC的中点,AC⊥BD,BD=8.

①求证:BD⊥平面 ;
;
②求证:平面AED⊥平面BCD;
③求二面角B-AC-D的正切值.
 ,D∈
,D∈ ,
, ,E为BC的中点,AC⊥BD,BD=8.
,E为BC的中点,AC⊥BD,BD=8.
①求证:BD⊥平面
 ;
;②求证:平面AED⊥平面BCD;
③求二面角B-AC-D的正切值.
①AB是AC在平面β上的射影,由AC⊥BD得AB⊥BD.∵α⊥β.∴DB⊥α.
②由AB=AC,且E是BC中点,得AE⊥BC,又AE⊥DB,故AE⊥平面BCD,因此可证得平面AED⊥平面BCD.
③设F是AC中点,连BF,DF.由于△ABC是正三角形,故BF⊥AC.又由DB⊥平面α,则DF⊥AC,∠BFD是二面角B-AC-D的平面角,
在Rt△BFD中,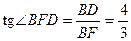 .
.
②由AB=AC,且E是BC中点,得AE⊥BC,又AE⊥DB,故AE⊥平面BCD,因此可证得平面AED⊥平面BCD.
③设F是AC中点,连BF,DF.由于△ABC是正三角形,故BF⊥AC.又由DB⊥平面α,则DF⊥AC,∠BFD是二面角B-AC-D的平面角,
在Rt△BFD中,
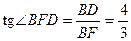 .
.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 的底面是边长为1的正方形,
的底面是边长为1的正方形, 底面
底面 ,
, 。
。
 ;
;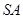 的中点为
的中点为 ,求异面直线
,求异面直线 与
与 所成角的大小;
所成角的大小; ,∠ACB=90°。
,∠ACB=90°。
 的8个顶点都在球
的8个顶点都在球 的表面上,
的表面上, 分别
分别 ,
, 的中点,则直线
的中点,则直线 被球
被球



 如图,直三棱柱
如图,直三棱柱 中,
中, ,
, 上有一动点
上有一动点 ,则
,则 周长的最小值为
周长的最小值为
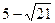


 底面ABCD,当
底面ABCD,当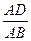 的值等于多少时,能使PB
的值等于多少时,能使PB
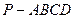 中,
中, 平面
平面 ,底面
,底面 .
.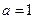 时,求证:
时,求证: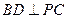 ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.