题目内容
(本小题满分14分) 如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.


(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且 ,
, ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.

|

|

(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且
 ,
, ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
(Ⅰ) 略 (Ⅱ)CF= cm
cm
 cm
cm:(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形(如下图)----2分


其面积为:6×6= 36(cm2)---4分
36(cm2)---4分
(注:图正确,面积计算体现了图形为正方形一样给分) (2)如图,以C为原点,CD为x轴,CB为y轴,CP为Z轴建立空间直角坐标系,则D(6,0,0),A(6,6,0),B(0,6,0),P(0,0,6),E(0,3,3),L(0,1,5),M(3,3,3),N(3,0,3)------6分
∴ ----7分
----7分
设平面LMN的法向量为 =(x,y,z
=(x,y,z )
)
由 得
得 令x="2" 则
令x="2" 则 =(2,0,3)----9分
=(2,0,3)----9分
设 ,---10分
,---10分
则
 ----11分
----11分
由 ,得
,得 ,即
,即 =
= ---12分
---12分
又EF 所以,EF//平面LMN----13分
所以,EF//平面LMN----13分
即在底面正方形的对角线AC上存在符合题意的点F,CF= AC=
AC= cm----14分
cm----14分


其面积为:6×6=
 36(cm2)---4分
36(cm2)---4分
|
∴
 ----7分
----7分设平面LMN的法向量为
 =(x,y,z
=(x,y,z )
)由
 得
得 令x="2" 则
令x="2" 则 =(2,0,3)----9分
=(2,0,3)----9分设
 ,---10分
,---10分则

 ----11分
----11分由
 ,得
,得 ,即
,即 =
= ---12分
---12分又EF
 所以,EF//平面LMN----13分
所以,EF//平面LMN----13分即在底面正方形的对角线AC上存在符合题意的点F,CF=
 AC=
AC= cm----14分
cm----14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 底面ABCD,当
底面ABCD,当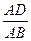 的值等于多少时,能使PB
的值等于多少时,能使PB
 的斜线
的斜线 交
交 ,过定点
,过定点 的动直线
的动直线 与
与 ,则动点
,则动点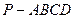 中,
中, 平面
平面 ,底面
,底面 .
.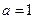 时,求证:
时,求证: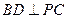 ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
 所在平面外一点,PA、PB、PC与平面ABC所的角均相等,又PA与BC垂直,那么
所在平面外一点,PA、PB、PC与平面ABC所的角均相等,又PA与BC垂直,那么 中,
中, 平面
平面 ,底面
,底面 =60
=60 ,
, ,
, 是线段
是线段 的中点.
的中点. ;
; 与平面
与平面 所成锐二面角的大小;
所成锐二面角的大小; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面PAE,并给出证明.
∥平面PAE,并给出证明.
 ,甲、乙两地均在本初子午线(
,甲、乙两地均在本初子午线( 经线上),且甲地位于北纬
经线上),且甲地位于北纬 ,乙地位于南纬
,乙地位于南纬 ,则甲、乙两地的球面距离为
,则甲、乙两地的球面距离为