题目内容
【题目】如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2. 
(1)求证:平面ABF⊥平面PQFE;
(2)若PQ与平面ABF所成的角为 ![]() ,求三棱锥P﹣QDE的体积.
,求三棱锥P﹣QDE的体积.
【答案】
(1)证明:如图,
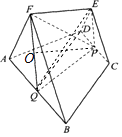
∵ABF为正三角形,且Q为AB的中点,∴FQ⊥AB,
在等腰梯形ABCD中,∵P、Q分别是CD、AB的中点,
∴PQ⊥AB,又FQ∩PQ=Q,∴AB⊥平面PEFQ,
又AB面ABF,∴平面ABF⊥平面PQFE
(2)解:取FQ中点O,连接PO,∵PQ=PF,∴PO⊥QF,
又平面ABF⊥平面PQFE,且平面ABF∩平面PQFE=QF,
∴PO⊥平面ABF,则∠PQO为PQ与平面ABF所成的角为 ![]() ,
,
∵等边三角形ABF的边长为2,∴QF= ![]() ,则OQ=
,则OQ= ![]() ,则OP=
,则OP= ![]() .
.
∴ ![]() ,
,
则 ![]() .
.
【解析】(1)由ABF为正三角形,且Q为AB的中点,可得FQ⊥AB,再由已知得PQ⊥AB,利用线面垂直的判定可得AB⊥平面PEFQ,再由面面垂直的判定可得平面ABF⊥平面PQFE;(2)取FQ中点O,连接PO,可得∠PQO为PQ与平面ABF所成的角为 ![]() ,求出OP=
,求出OP= ![]() .得到三角形QPE的面积,然后利用等积法求得三棱锥P﹣QDE的体积.
.得到三角形QPE的面积,然后利用等积法求得三棱锥P﹣QDE的体积.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
相关题目
