题目内容
(本题满分12分)已知命题 函数
函数 的定义域是R;命题q:方程
的定义域是R;命题q:方程 有两个不相等的实数解,若“p且非q”为真,求实数
有两个不相等的实数解,若“p且非q”为真,求实数 的取值范围。
的取值范围。
 函数
函数 的定义域是R;命题q:方程
的定义域是R;命题q:方程 有两个不相等的实数解,若“p且非q”为真,求实数
有两个不相等的实数解,若“p且非q”为真,求实数 的取值范围。
的取值范围。解:由题意,若p为真命题, 则mx2-2x+m>0对任意实数x都成立,……2分
若m=0,显然不成立.……3分
若m≠0,则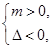 解得:m>3. ……………………6分
解得:m>3. ……………………6分
命题q:方程x2+mx+9=0有两个不相等的实数解,则△>0,解得:m<-6,m>6, 8分
若“p且非q”为真,则p真q假…………9分
故有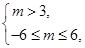 ∴3<m≤6,…………11分
∴3<m≤6,…………11分
故实数a的取值范围为(3,6].…………12分
若m=0,显然不成立.……3分
若m≠0,则
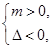 解得:m>3. ……………………6分
解得:m>3. ……………………6分命题q:方程x2+mx+9=0有两个不相等的实数解,则△>0,解得:m<-6,m>6, 8分
若“p且非q”为真,则p真q假…………9分
故有
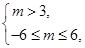 ∴3<m≤6,…………11分
∴3<m≤6,…………11分故实数a的取值范围为(3,6].…………12分
略

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
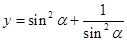 的最小值是4
的最小值是4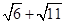 >
>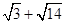
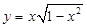 的最大值是
的最大值是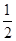
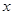 >0且
>0且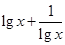 ≥2
≥2 :关于
:关于 的函数
的函数 在[1,+∞)上是增函数,命题
在[1,+∞)上是增函数,命题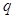 :关于
:关于 在R上为减函数,若
在R上为减函数,若 的取值范是 .
的取值范是 .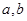 ,如果
,如果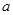 平行于平面
平行于平面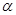 ,那么
,那么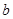 不平行平面
不平行平面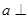 平面
平面 ”的否定是 ▲
”的否定是 ▲  (1)
(1) 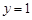 ;(2)
;(2)  ;(3)
;(3)  ;
;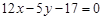
 “相关直线 ”的是 (只填序号)
“相关直线 ”的是 (只填序号) 是
是 的充分条件
的充分条件 是
是 的充分条件
的充分条件 ,则
,则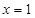 ”的逆否命题是“若
”的逆否命题是“若 ,则
,则 ”;
”; ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件; ”为假命题,则
”为假命题,则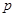 、
、 均为假命题;
均为假命题; ,使得
,使得 ,则
,则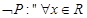 ,均有
,均有 ;
;