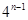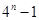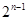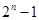题目内容
设an=1+q+q2+…+qn-1(n∈N,q≠±1),An=C n1a1+C n2a2+…+Cnnan,求An(用n和q表示).
An=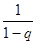 [2n-(1-q)n]
[2n-(1-q)n]
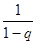 [2n-(1-q)n]
[2n-(1-q)n]解:因为an=
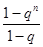 ,
,所以An=
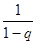 [C n1 (1-q)+C n2 (1-q2)+…+Cnn (1-qn)]
[C n1 (1-q)+C n2 (1-q2)+…+Cnn (1-qn)]=
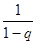 [C n1+C n2+…+Cnn-(Cn1q+Cn2q2+…+Cnnqn)]
[C n1+C n2+…+Cnn-(Cn1q+Cn2q2+…+Cnnqn)]=
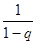 [(2n-1)-(1+q)n+1]
[(2n-1)-(1+q)n+1]=
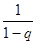 [2n-(1-q)n].
[2n-(1-q)n].
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 各项都是正数,
各项都是正数, ,
,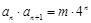 ,
,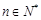 .
.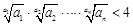 .
.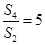 , 则数列{
, 则数列{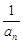 }的前5项和为( )
}的前5项和为( )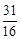
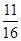
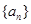 的各项都是正数,且
的各项都是正数,且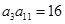 则
则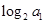 = ( )
= ( )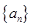 中,
中,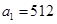 ,公比
,公比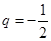 ,用
,用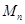 表示它的前
表示它的前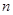 项之积,即
项之积,即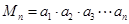 ,则数列
,则数列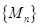 中的最大项是( )
中的最大项是( )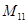
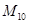
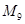
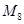
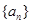 的前n项和为
的前n项和为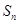 ,且
,且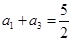 ,
,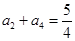 ,则
,则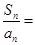 ( )
( )