题目内容
(本小题满分12分)已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线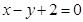 上。
上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn.
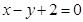 上。
上。(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn.
解:(1)∵an是Sn与2的等差中项 ∴Sn=2an-2 ∴a1=S1=2a1-2,
解得a1="2" a1+a2=S2=2a2-2,解得a2="4"
(2)∵Sn=2an-2,Sn-1=2an-1-2,又Sn—Sn-1=an,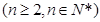 ∴an=2an-2an-1,
∴an=2an-2an-1,
又an≠0, ∴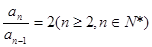 ,即数列{an}是等比数列
,即数列{an}是等比数列
∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1,
(3)∵cn=(2n-1)2n ∴Tn=a1b1+ a2b2+····anbn=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
则 -Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6
解得a1="2" a1+a2=S2=2a2-2,解得a2="4"
(2)∵Sn=2an-2,Sn-1=2an-1-2,又Sn—Sn-1=an,
 ∴an=2an-2an-1,
∴an=2an-2an-1, 又an≠0, ∴
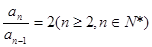 ,即数列{an}是等比数列
,即数列{an}是等比数列 ∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1,
(3)∵cn=(2n-1)2n ∴Tn=a1b1+ a2b2+····anbn=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
则 -Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 Sn-1 (n≥2),则Sn= .
Sn-1 (n≥2),则Sn= .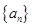 的前
的前 项和为
项和为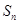 ,若对任意的
,若对任意的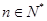 ,有
,有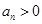 且
且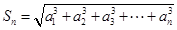 成立.
成立.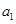 、
、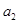 的值;
的值;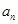 ;
;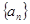 的前
的前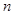 项和为
项和为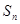 ,令
,令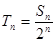 ,若对一切正整数
,若对一切正整数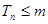 ,求
,求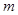 的取值范围.
的取值范围.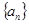 满足
满足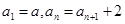 。定义数列
。定义数列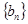 ,使得
,使得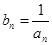 ,
,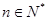 。若4<
。若4<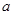 < 6,则数列
< 6,则数列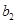
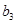
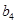
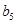
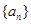 的各项均为正数,且
的各项均为正数,且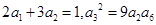 .
.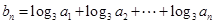 ,求数列
,求数列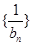 的前n项和.
的前n项和.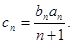 ,求数列{
,求数列{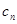 }的前
}的前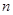 项和.
项和.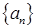 的通项公式为
的通项公式为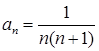 ,则前10项和
,则前10项和 ;
;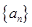 满足
满足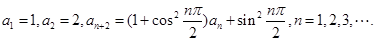
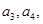 并求数列
并求数列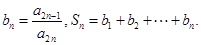 ,求
,求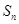
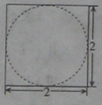



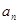 }的前n项和
}的前n项和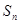 =n2,{
=n2,{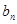 }为等比数列,且
}为等比数列,且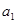 =
=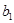 ,
,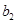 (
( -
-