题目内容

20．i为虚数单位，复平面内表示复数z=$\frac{1}{3+i}$的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数代数形式的乘除运算化简，求出z的坐标得答案．

解答 解：∵z=$\frac{1}{3+i}$=$\frac{3-i}{（3+i）（3-i）}=\frac{3}{10}-\frac{1}{10}i$，
∴复平面内表示复数z=$\frac{1}{3+i}$的点的坐标为（$\frac{3}{10}，-\frac{1}{10}$），位于第四象限．
故选：D．

点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案
相关题目
10．已知点A（$\frac{π}{8}$，f（$\frac{π}{8}$））和直线x=$\frac{3π}{8}$分别是函数f（x）=2$\sqrt{2}$sin?xsin（?x+$\frac{π}{4}$）（?＞0）相邻的一个对称中心和一条对称轴，将函数f（x）的图象向右平移φ个单位得到函数g（x）的图象，若当x=$\frac{π}{3}$时，g（x）取最大值，则g（x）在[-$\frac{π}{2}$，0]上单调增区间为[-$\frac{π}{6}$，0]．
11．已知函数f（x）=（m-2）x2+mx+（2m+1）的两个零点分别在区间（-1，0）和区间（1，2）内，则实数m的取值范围是（　　）
A．[$\frac{1}{4}$，$\frac{1}{2}$]B．（$\frac{1}{4}$，$\frac{1}{2}$）C．（-$\frac{1}{2}$，$\frac{1}{4}$）D．（$\frac{1}{4}$，$\frac{1}{2}$）
8．若向量$\overrightarrow{a}$=（x，3）（x∈R），则“x=4是|$\overrightarrow{a}$|=5”的（　　）
A．充要条件B．必要不充分条件
C．充分不必要条件D．既不充分也不必要条件
15．设某几何体的三视图如图，则该几何体的体积为4
5．设函数fn（x）=n2x2（1-x）n（n为正整数），则fn（x）在[0，1]上的最大值为（　　）
A．0B．1C．（1-$\frac{2}{2+n}$）nD．4（$\frac{2}{2+n}$）n+2
12．把函数y=sin（2x+$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位得到函数f（x）的图象，则下列说法正确的是（　　）
A．f（x）的图象关于y轴对称B．f（x）的图象关于原点对称
C．f（x）的图象关于直线x=$\frac{π}{3}$对称D．f（x）的图象关于点（$\frac{π}{3}$，0）对称
9．已知双曲线C与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点F1、F2，点P为双曲线C与椭圆的一个交点，且满足|PF1|=2|PF2|，则双曲线C的渐近线方程是（　　）
A．y=±$\sqrt{3}$xB．y=±$\sqrt{2}$xC．y=±xD．y=±$\frac{\sqrt{3}}{2}$x
10．如图，有一个几何体的三视图及其尺寸（单位：cm），则该几何体的表面积和体积分别为（　　）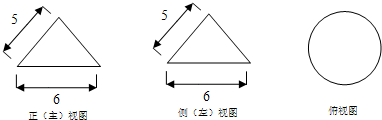
A．24πcm2，12πcm3B．15πcm2，12πcm3C．24πcm2，36πcm3D．15πcm2，36πcm3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网