题目内容
1.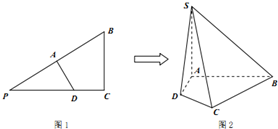 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求平面SAB与平面SCD所成锐二面角的余弦值.
分析 (Ⅰ)证明SA⊥AB,SA⊥AD,即可证明SA⊥平面ABCD;
(Ⅱ)延长BA,CD相交于P,连接SP,取SP的中点M,连接MA,MD,证明∠AMD为平面SAB与平面SCD所成锐二面角的平面角,求出MA,MD,即可求平面SAB与平面SCD所成锐二面角的余弦值.
解答  (Ⅰ)证明:在直角三角形PBC中,PC=4,BC=3,PD:DC=5:3,
(Ⅰ)证明:在直角三角形PBC中,PC=4,BC=3,PD:DC=5:3,
所以PB=5,PD=2.5,DC=1.5,
因为∠PAD=∠C=90°,∠P=∠P,
所以△PAD∽△PCB,
所以$\frac{PA}{AC}=\frac{PD}{PB}=\frac{AD}{BC}$,
所以PA=2,AB=PB-PA=3,AD=1.5,
△SAB中,SA=PA=2,SB=$\sqrt{13}$,
所以SA2+AB2=SB2,
所以SA⊥AB
因为AD∥PB,
所以SA⊥AD,
因为AB∩AD=A,
所以SA⊥平面ABCD;
(Ⅱ)解:在图2中,延长BA,CD相交于P,连接SP,取SP的中点M,连接MA,MD,则
因为PA=SA,PD=SD,
所以MA⊥SP,MD⊥SP,
所以∠AMD为平面SAB与平面SCD所成锐二面角的平面角,
因为SA⊥AD,AD⊥PB,SA∩PB=A,
所以AD⊥平面SPB,
因为MA?平面SPB,
所以AD⊥MA.
在直角三角形SPA中,PA=SA=2,M为SP的中点,
所以SP=2$\sqrt{2}$,MA=$\sqrt{2}$,
在△SPD中,PD=SD=2.5,M为SP中点,所以MD=$\frac{\sqrt{17}}{2}$,
所以cos∠AMP=$\frac{MA}{MD}$=$\frac{2\sqrt{34}}{17}$,
所以平面SAB与平面SCD所成锐二面角的余弦值为$\frac{2\sqrt{34}}{17}$.
点评 考查线面垂直的性质于判定定理,考查平面SAB与平面SCD所成锐二面角的余弦值,考查学生分析解决问题的能力,属于中档题.

| an | bn | an•bn | 判断{an•bn}是否是等比数列 | |
| 例 | 3×($\frac{2}{3}$)n | -5×2n-1 | -10×($\frac{4}{3}$)n-1 | 是 |
| 自选1 | ||||
| 自选2 |
| f (1)=-2 | f (1.5)=0.625 | f (1.25)=-0.984 |
| f (1.375)=-0.260 | f (1.4375)=0.162 | f (1.40625)=-0.054 |
| A. | 1.25 | B. | 1.375 | C. | 1.42 | D. | 1.5 |
| A. | $\frac{25}{4}$ | B. | $\frac{15}{2}$ | C. | 4 | D. | 6 |
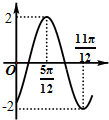
| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
| A. | {2} | B. | {1,2} | C. | {3,5} | D. | {4,5} |
| A. | x2+y2=2 | B. | x2+y2=$\frac{9}{4}$ | C. | x2+y2=4 | D. | x2+y2=9 |
| A. | [$\frac{1}{4}$,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,$\frac{1}{4}$) | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |