题目内容
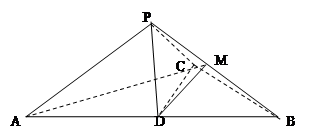
在如图所示的几何体中,四边形ABCD为正方形, 为直角三角形,
为直角三角形, ,且
,且 .
.

(1)证明:平面 平面
平面 ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
 为直角三角形,
为直角三角形, ,且
,且 .
.
(1)证明:平面
 平面
平面 ;
;(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
(1)详见解析;(2) .
.
 .
.试题分析:(1)由已知可知AE⊥AB,又AE⊥AD,所以AE⊥平面ABCD,所以AE⊥DB,又ABCD为正方形,所以DB⊥AC,所以DB⊥平面AEC,而BD
 平面BED,故有平面AEC⊥平面BED.
平面BED,故有平面AEC⊥平面BED.(2)作DE的中点F,连接OF,AF,由于O是DB的中点,且OF∥BE,可知∠FOA或其补角是异面直线BE与AC所成的角;设正方形ABCD的边长为2
 ,则
,则 ,由于
,由于 ,AB=2AE,
,AB=2AE,可知
 ,
, ,则
,则 ,又
,又 ,∴
,∴ =
= ,由余弦定理的推理∴
,由余弦定理的推理∴ ∠FOA=
∠FOA= =
= ,故异面直线BE与AC所成的角的余弦值为
,故异面直线BE与AC所成的角的余弦值为 .
.试题解析:(1)由已知有AE⊥AB,又AE⊥AD,
所以AE⊥平面ABCD,所以AE⊥DB, 3分
又ABCD为正方形,所以DB⊥AC, 4分
所以DB⊥平面AEC,BD
 面BED
面BED故有平面AEC⊥平面BED. 6分
(2)作DE的中点F,连接OF,AF,

∵O是DB的中点,
∴OF∥BE,∴∠FOA或其补角是异面直线BE与AC所成的角。 8分
设正方形ABCD的边长为2
 ,
,则
 , 9分
, 9分∵
 ,AB=2AE,
,AB=2AE,∴
 ,
, ,∴
,∴ 10分
10分又
 ,∴
,∴ =
= ,∴
,∴ ∠FOA=
∠FOA= =
=
∴异面直线BE与AC所成的角的余弦值为
 12分.
12分.
练习册系列答案
相关题目
 .
.

 .
.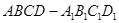 ,点
,点 ,
,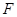 ,
,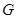 分别是线段
分别是线段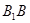 ,
,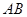 和
和 上的动点,观察直线
上的动点,观察直线 与
与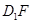 ,
,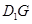 .给出下列结论:
.给出下列结论: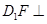

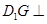

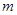 ,
,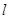 和平面
和平面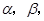 且
且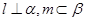 ,给出下列四个命题:
,给出下列四个命题: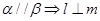 ②
②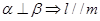 ③
③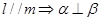 ④
④