题目内容
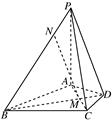
如图,在四棱锥PABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.

(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.

(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
见解析
(1)∵PA⊥底面ABCD,∴PA⊥BC,
又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.(3分)
又BC?平面PCB,
∴平面PAB⊥平面PCB.(6分)
(2)∵PA⊥底面ABCD,又AD?平面ABCD,
∴PA⊥AD.
又∵PC⊥AD,又PC∩PA=P,∴AD⊥平面PAC,又AC?平面PAC,
∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=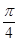 ,
,
∴∠DCA=∠BAC=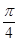 又AC⊥AD,故△DAC为等腰直角三角形.(4分)
又AC⊥AD,故△DAC为等腰直角三角形.(4分)
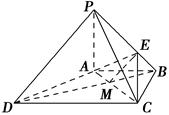
∴DC=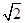 AC=
AC=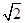 (
(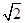 AB)=2AB.
AB)=2AB.
连接BD,
交AC于点M,则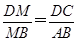 =2.
=2.
在△BPD中,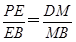 =2,
=2,
∴PD∥EM
又PD?平面EAC,EM?平面EAC,
∴PD∥平面EAC.(14分)
又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.(3分)
又BC?平面PCB,
∴平面PAB⊥平面PCB.(6分)
(2)∵PA⊥底面ABCD,又AD?平面ABCD,
∴PA⊥AD.
又∵PC⊥AD,又PC∩PA=P,∴AD⊥平面PAC,又AC?平面PAC,
∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=
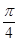 ,
,∴∠DCA=∠BAC=
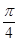 又AC⊥AD,故△DAC为等腰直角三角形.(4分)
又AC⊥AD,故△DAC为等腰直角三角形.(4分)∴DC=
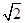 AC=
AC=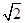 (
(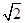 AB)=2AB.
AB)=2AB.连接BD,

交AC于点M,则
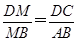 =2.
=2. 在△BPD中,
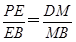 =2,
=2,∴PD∥EM
又PD?平面EAC,EM?平面EAC,
∴PD∥平面EAC.(14分)

练习册系列答案
相关题目

 平面
平面 .
. 平面
平面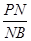 =
=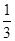 .
.

 为直角三角形,
为直角三角形, ,且
,且 .
.
 平面
平面 ;
; ACD沿AC折起至
ACD沿AC折起至 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

 平面BGH;
平面BGH;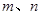 是两条不同的直线,
是两条不同的直线,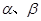 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )



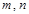 为两条不同直线,
为两条不同直线,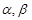 为两个不同平面,给出下列命题:
为两个不同平面,给出下列命题: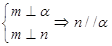 ②
②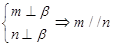
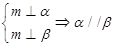 ④
④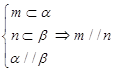
 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: 则
则 或
或 ;
; 则
则 ;
; 不垂直于
不垂直于 ,则
,则 且
且 则
则
 ;
; 且
且 则
则 .
.