题目内容
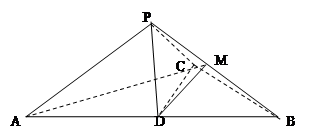
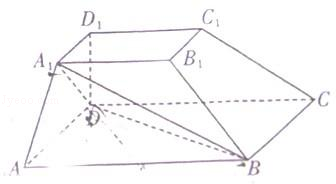
如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。
 .
.
(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
 .
.(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
(1)详见解析,(2)详见解析,(3)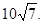
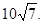
试题分析:(1)证线面平行找线线平行,本题有中点条件,可利用中位线性质.即DM∥AP,写定理条件时需完整,因为若缺少DM
 面APC,,则DM可能在面PAC内,若缺少AP
面APC,,则DM可能在面PAC内,若缺少AP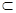 面APC,则DM与面PAC位置关系不定.(2)证面面垂直关键找线面垂直.可由面面垂直性质定理探讨,因为BC垂直AC,而AC为两平面的交线,所以应有BC垂直于平面PAC,这就是本题证明的首要目标.因为BC垂直AC,因此只需证明BC垂直平面PAC另一条直线.这又要利用线面垂直与线线垂直关系转化.首先将题目中等量关系转化为垂直条件,即DM⊥PB,从而有PA⊥PB,而PA⊥PC,所以PA⊥面PBC,因此PA⊥BC.(3)求锥的体积关键找出高,有(2)有PA⊥面PBC,因此DM为高,利用体积公式可求得
面APC,则DM与面PAC位置关系不定.(2)证面面垂直关键找线面垂直.可由面面垂直性质定理探讨,因为BC垂直AC,而AC为两平面的交线,所以应有BC垂直于平面PAC,这就是本题证明的首要目标.因为BC垂直AC,因此只需证明BC垂直平面PAC另一条直线.这又要利用线面垂直与线线垂直关系转化.首先将题目中等量关系转化为垂直条件,即DM⊥PB,从而有PA⊥PB,而PA⊥PC,所以PA⊥面PBC,因此PA⊥BC.(3)求锥的体积关键找出高,有(2)有PA⊥面PBC,因此DM为高,利用体积公式可求得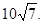
试题解析:(1)D为AB中点,M为PB中点
 DM∥AP
DM∥AP又
 DM
DM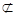 面APC,AP
面APC,AP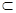 面APC
面APC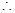 DM∥面PAC
DM∥面PAC(2)
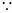 △PDB是正三角形,M为PB中点
△PDB是正三角形,M为PB中点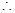 DM⊥PB,又
DM⊥PB,又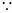 DM∥AP,
DM∥AP,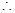 PA⊥PB
PA⊥PB又
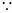 PA⊥PC,PB
PA⊥PC,PB PC=P,PA⊥面PBC
PC=P,PA⊥面PBC又
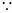 BC
BC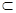 面PBC,
面PBC,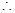 PA⊥BC
PA⊥BC又
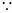 ∠ACB=90°,
∠ACB=90°,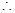 BC⊥AC
BC⊥AC又
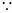 AC
AC PA=A,
PA=A,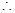 BC⊥面PAC
BC⊥面PAC又
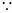 BC
BC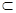 面ABC,
面ABC,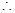 面PAC⊥面ABC
面PAC⊥面ABC(3)
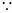 AB=20,D为AB中点,AP⊥面PBC
AB=20,D为AB中点,AP⊥面PBC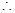 PD=10
PD=10又
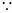 △PDB为正三角形,
△PDB为正三角形,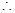 DM=5
DM=5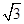
又
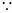 BC=4,PB=10,
BC=4,PB=10, PC=2
PC=2
 S△PBC=
S△PBC=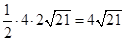
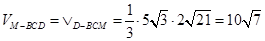

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 中,侧面
中,侧面 ⊥底面
⊥底面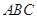 ,侧棱
,侧棱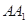 与底面
与底面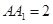 .底面
.底面 点,
点,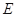 是线段
是线段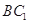 上一点,且
上一点,且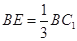 .
.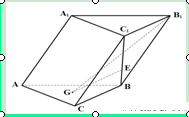
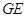 //侧面
//侧面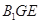 与底面
与底面 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面
 平面
平面 .
. 平面
平面 为直角三角形,
为直角三角形, ,且
,且 .
.
 平面
平面 ;
;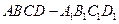 的棱长为a,M、N分别为
的棱长为a,M、N分别为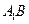 和AC上的点,
和AC上的点,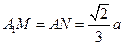 ,则MN与平面
,则MN与平面 的位置关系是( )
的位置关系是( )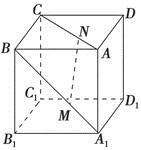
 是两条不同的直线,
是两条不同的直线,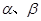 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )



 平面
平面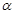 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面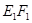 长的范围是( )
长的范围是( ) ]
] ,
, ,
, ,
,