题目内容
已知直线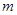 ,
,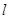 和平面
和平面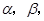 且
且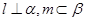 ,给出下列四个命题:
,给出下列四个命题:
①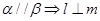 ②
②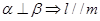 ③
③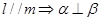 ④
④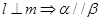
其中真命题的有________(请填写全部正确命题的序号)
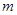 ,
,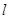 和平面
和平面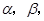 且
且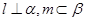 ,给出下列四个命题:
,给出下列四个命题:①
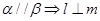 ②
②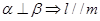 ③
③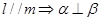 ④
④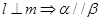
其中真命题的有________(请填写全部正确命题的序号)
①③
试题分析:在①中由

 得
得 ,又
,又 ,故
,故 ;
;在②中
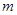 可在平面
可在平面 内任意转动,故
内任意转动,故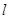 与
与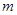 关系不确定;
关系不确定;在③中,由
 ,
, 得
得 ,又因为
,又因为 ,故
,故 ;
;在④中,平面
 可绕
可绕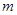 转动,故
转动,故 与
与 关系不确定.
关系不确定.
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目

 平面
平面 .
. 平面
平面 为直角三角形,
为直角三角形, ,且
,且 .
.
 平面
平面 ;
; 中,底面
中,底面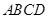 是边长为
是边长为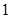 的正方形,
的正方形, ,
,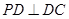 ,且
,且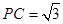 .
.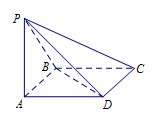
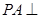 平面
平面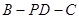 的余弦值;
的余弦值;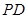 上是否存在一点
上是否存在一点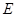 ,使直线
,使直线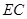 与平面
与平面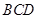 所成的角是
所成的角是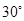 ?若存在,求
?若存在,求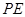 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
. ACD沿AC折起至
ACD沿AC折起至 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

 平面BGH;
平面BGH;

 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: 则
则 或
或 ;
; 则
则 ;
; 不垂直于
不垂直于 ,则
,则 且
且 则
则
 ;
; 且
且 则
则 .
. 中,
中, 分别是
分别是 的中点,则四边形
的中点,则四边形 是( )
是( )