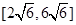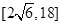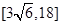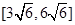题目内容
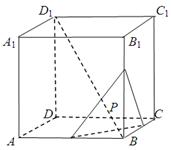
如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.

(1)求证:PC⊥BC
(2)求点A到平面PBC的距离.

(1)求证:PC⊥BC
(2)求点A到平面PBC的距离.
(1)BC⊥PC;(2) .
.
 .
.试题分析:(1)要证线线垂直,要从线面垂直角度入手,根据题中所给条件易知BC⊥平面PDC,而PC在平面PDC,从而能够证明出BC⊥PC. (2)要求点到面的距离,常用到等体积定理,由已知条件可知
VA-PBC=VP-ABC ,而通过计算可知VP-ABC=
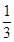 S△ABC·PD=
S△ABC·PD=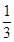 ,接下来只需要求出△PBC的面积,这样根据
,接下来只需要求出△PBC的面积,这样根据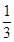 S△PBC·h=
S△PBC·h=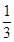 ,∴h=
,∴h= ,所以点A到平面PBC的距离为
,所以点A到平面PBC的距离为 .
.试题解析:(1)∵PD⊥平面ABCD,BC?平面ABCD,∴PD⊥BC.
由∠BCD=90°知,BC⊥DC,
∵PD∩DC=D,∴BC⊥平面PDC,
∴BC⊥PC.
(2)设点A到平面PBC的距离为h,
∵AB∥DC,∠BCD=90°,∴∠ABC=90°,
∵AB=2,BC=1,∴S△ABC=
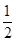 AB·BC=1,
AB·BC=1,∵PD⊥平面ABCD,PD=1,
∴VP-ABC=
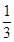 S△ABC·PD=
S△ABC·PD=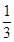 ,
,∵PD⊥平面ABCD,∴PD⊥DC,
∵PD=DC=1,∴PC=
 ,
,∵PC⊥BC,BC=1,
∴S△PBC=
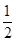 PC·BC=
PC·BC=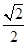 ,
,∵VA-PBC=VP-ABC,
∴
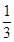 S△PBC·h=
S△PBC·h=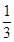 ,∴h=
,∴h= ,
,∴点A到平面PBC的距离为
 .
.
练习册系列答案
相关题目
 为直角三角形,
为直角三角形, ,且
,且 .
.
 平面
平面 ;
; 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
. ACD沿AC折起至
ACD沿AC折起至 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

 平面BGH;
平面BGH;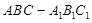 中,
中,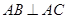 ,
,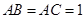 ,
,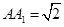 ,D为BC中点.
,D为BC中点.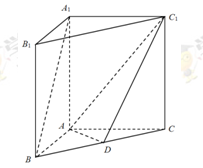
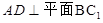 ;
; ;
;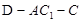 的正弦值.
的正弦值.

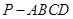 的底面
的底面 为矩形,且
为矩形,且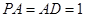 ,
,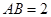 ,
,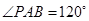 ,
,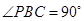 ,
,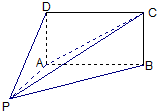
 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,下列命题:
是三个不同的平面,下列命题: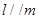 ,
,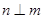 ,则
,则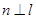 ; ②若
; ②若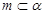 ,则
,则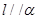 ;
;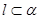 ,
,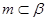 ,
,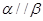 ,则
,则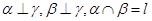 ,则
,则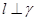 .
.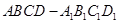 的棱长为
的棱长为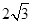 ,动点P在对角线
,动点P在对角线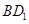 上,过点P作垂直于
上,过点P作垂直于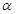 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设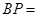 x,则当
x,则当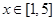 时,函数
时,函数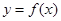 的值域为( )
的值域为( )