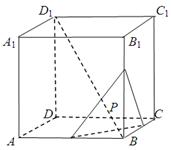
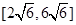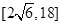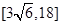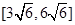题目内容
已知正方体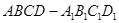 ,点
,点 ,
,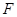 ,
,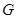 分别是线段
分别是线段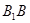 ,
,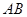 和
和 上的动点,观察直线
上的动点,观察直线 与
与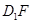 ,
, 与
与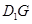 .给出下列结论:
.给出下列结论:
①对于任意给定的点 ,存在点
,存在点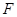 ,使得
,使得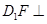
 ;
;
②对于任意给定的点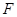 ,存在点
,存在点 ,使得
,使得
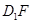 ;
;
③对于任意给定的点 ,存在点
,存在点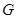 ,使得
,使得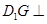
 ;
;
④对于任意给定的点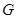 ,存在点
,存在点 ,使得
,使得
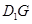 .
.

其中正确结论的个数是( )
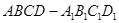 ,点
,点 ,
,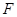 ,
,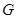 分别是线段
分别是线段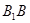 ,
,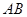 和
和 上的动点,观察直线
上的动点,观察直线 与
与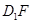 ,
, 与
与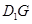 .给出下列结论:
.给出下列结论:①对于任意给定的点
 ,存在点
,存在点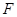 ,使得
,使得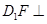
 ;
;②对于任意给定的点
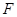 ,存在点
,存在点 ,使得
,使得
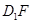 ;
;③对于任意给定的点
 ,存在点
,存在点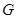 ,使得
,使得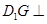
 ;
;④对于任意给定的点
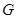 ,存在点
,存在点 ,使得
,使得
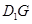 .
.
其中正确结论的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
B
试题分析:因为对任意的E点,则直线CE所形成的轨迹都在平面
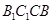 上,所以要使得
上,所以要使得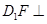
 ,即要存在
,即要存在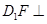 平面
平面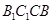 ,显然是不成立的,所以①不正确;因为对于任意点
,显然是不成立的,所以①不正确;因为对于任意点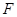 ,由
,由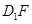 形成的轨迹在平面
形成的轨迹在平面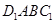 上,所以要存在
上,所以要存在
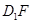 只需要
只需要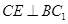 即可,这显然可以成立,所以②正确.同理③只要G点移到
即可,这显然可以成立,所以②正确.同理③只要G点移到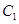 点即可成立,所以③正确.与①类似④不成立.故选B.
点即可成立,所以③正确.与①类似④不成立.故选B.
练习册系列答案
相关题目
 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面
 为直角三角形,
为直角三角形, ,且
,且 .
.
 平面
平面 ;
;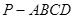 中,底面
中,底面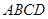 为矩形,
为矩形,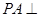 平面
平面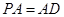 ,
,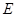 为
为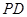 中点.
中点.
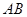 //平面
//平面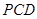 ;
;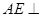 平面
平面 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
. 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: 则
则 或
或 ;
; 则
则 ;
; 不垂直于
不垂直于 ,则
,则 且
且 则
则
 ;
; 且
且 则
则 .
. 中,
中, 分别是
分别是 的中点,则四边形
的中点,则四边形 是( )
是( )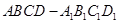 的棱长为
的棱长为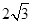 ,动点P在对角线
,动点P在对角线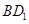 上,过点P作垂直于
上,过点P作垂直于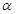 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设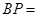 x,则当
x,则当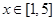 时,函数
时,函数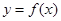 的值域为( )
的值域为( )