题目内容
19．
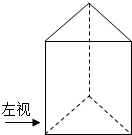如图，侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2，则该正三棱柱的侧面积为（ ）| A． | 3a2 | B． | 4a2 | C． | 6a2 | D． | 8a2 |
分析 利用三视图侧视图面积求出三棱柱底面正三角形的高，然后求出底面三角形的边长，即可求解侧面积．
解答 解：由题意可知侧视图是矩形，面积为：2ah=$\sqrt{3}$a2，可得h=$\frac{\sqrt{3}a}{2}$，底面正三角形的高为：$\frac{\sqrt{3}a}{2}$，底面三角形的边长为：a，该正三棱柱的侧面积为：3a×2a=6a2．
故选：C．
点评 本题考查棱柱的侧面积的求法，几何体的三视图的应用，考查计算能力．
练习册系列答案
相关题目
9．已知函数f（x）=$\frac{1+lnx}{x}$在区间（a，a+$\frac{2}{3}$）（a＞0）上存在极值，则实数a的取值范围是（ ）
| A． | （0，1） | B． | （$\frac{1}{3}$，1） | C． | （$\frac{1}{2}$，1） | D． | （$\frac{2}{3}$，1） |
7．已知$a={log_3}\frac{1}{2}，b={2^{0.01}}，c=ln\frac{1}{2}$，则a，b，c的大小关系为（ ）
| A． | b＞a＞c | B． | b＞c＞a | C． | a＞c＞b | D． | a＞b＞c |
设全集为U=R，集合A={x|（x+3）（x-6）≤0}，B={x|log2（x+2）＜4}．