题目内容
已知函数f(x)=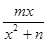 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的极值;
(3)设函数g(x)=x2-2ax+a,若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)≤f(x1),求实数a的取值范围.
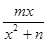 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.(1)求函数f(x)的解析式;
(2)求函数f(x)的极值;
(3)设函数g(x)=x2-2ax+a,若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)≤f(x1),求实数a的取值范围.
(1)f(x)=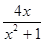
(2)当x=-1时,函数f(x)有极小值-2;当x=1时,函数f(x)有极大值2;
(3)a的取值范围为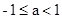
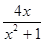
(2)当x=-1时,函数f(x)有极小值-2;当x=1时,函数f(x)有极大值2;
(3)a的取值范围为
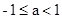
解:(1)∵函数f(x)=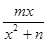 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.
∴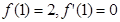 ,
,
又由f′(x)=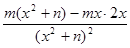 =
=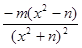 ,
,
由题意得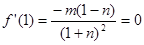
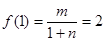 ,解得m=4,n=1,
,解得m=4,n=1,
经检验,当m=4,n=1时,函数f(x)在x=1处取得极小值2
∴函数f(x)的解析式为f(x)=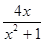 ;
;
(2)∵函数f(x)的定义域为R且由(1)有f′(x)=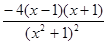
令f′(x)=0,解得:x=±1
∴当x变化时,f(x),f′(x)的变化情况如下表:
∴当x=-1时,函数f(x)有极小值-2;当x=1时,函数f(x)有极大值2;
(3)由(2)知函数f(x)的大致图象如图所示:

则f(x)在x=-1处取得极小值f(-1)=-2,
在x=1处取得极大值f(1)=2
又∵x>0时,f(x)>0,
∴f(x)的最小值为-2,∴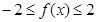
∵若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)≤f(x1)
∴当x∈[-1,1]时,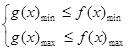
当a≤-1时,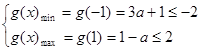 ,得a=-1,
,得a=-1,
当a≥1时,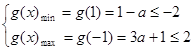 ,得无解.
,得无解.
当-1 <a< 1时,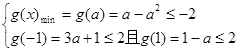 ,得-1 <a< 1.
,得-1 <a< 1.
综上所述.a的取值范围为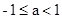 .
.
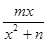 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.∴
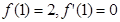 ,
,又由f′(x)=
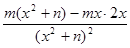 =
=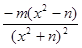 ,
,由题意得
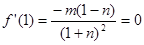
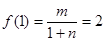 ,解得m=4,n=1,
,解得m=4,n=1,经检验,当m=4,n=1时,函数f(x)在x=1处取得极小值2
∴函数f(x)的解析式为f(x)=
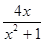 ;
;(2)∵函数f(x)的定义域为R且由(1)有f′(x)=
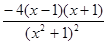
令f′(x)=0,解得:x=±1
∴当x变化时,f(x),f′(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 减 | 极小值-2 | 增 | 极大值2 | 减 |
(3)由(2)知函数f(x)的大致图象如图所示:

则f(x)在x=-1处取得极小值f(-1)=-2,
在x=1处取得极大值f(1)=2
又∵x>0时,f(x)>0,
∴f(x)的最小值为-2,∴
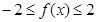
∵若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)≤f(x1)
∴当x∈[-1,1]时,
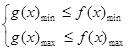
当a≤-1时,
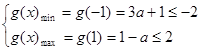 ,得a=-1,
,得a=-1,当a≥1时,
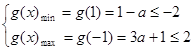 ,得无解.
,得无解.当-1 <a< 1时,
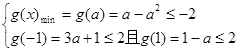 ,得-1 <a< 1.
,得-1 <a< 1.综上所述.a的取值范围为
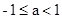 .
.
练习册系列答案
相关题目
 .
.
 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+ x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,
, 。
。 在
在 上的值域;
上的值域; ,对
,对 ,
, 恒成立,
恒成立, 的取值范围
的取值范围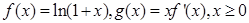 ,其中
,其中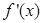 是
是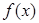 的导函数.
的导函数.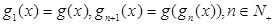 ,
,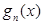 的表达式;
的表达式;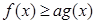 恒成立,求实数
恒成立,求实数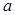 的取值范围;
的取值范围;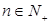 ,比较
,比较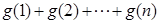 与
与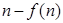 的大小,并加以证明.
的大小,并加以证明. 的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为
的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为 ,所做成的盒子体积为
,所做成的盒子体积为 (不计接缝)。
(不计接缝)。 为多少时,体积
为多少时,体积
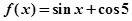 ,则该函数在点
,则该函数在点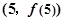 处切线的斜率等于( )
处切线的斜率等于( )


