题目内容
【题目】某市为了调查小区成年居民对环境治理情况的满意度（满分按100计），随机对20名六十岁以上的老人和20名十八岁以上六十岁以下的中青年进行了不记名的问卷调查，得到了如下统计结果：
表1：六十岁以上的老人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 1 | 5 | 6 | 5 | 3 |
表2：十八岁以上六十岁以下的中青年人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 2 | 4 | 8 | 4 | 2 |
表3：
满意度小于80 | 满意度不小于80 | 合计 | |
六十岁以上老人人数 | |||
十八岁以上六十岁以下的中青年人人数 | |||
合计 |
（1）若该小区共有中青年人500人，试估计其中满意度不少于80的人数；
（2）完成表3的
列联表，并回答能否有
的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”？
（3）从表3的六十岁以上的老人“满意度小于80”和“满意度不小于80”的人数中用分层抽样的方法抽取一个容量为5的样本，再从中任取3人，求至少有两人满意小于80的概率.
附：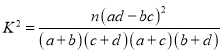
，其中
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
【答案】（1）
；（2）没有
的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”；（3）
.
【解析】
（1）根据抽样比例求得抽取满意度不少于80的人数；
（2）填写列联表，计算观测值，对照临界值得出结论；
（3）利用分层抽样方法抽取样本，利用列举法求出基本事件数，计算所求的概率值．
解：（1）根据表中数据知，20人中满意度不少于80的人数为6人，
该小区中青年人500人中，满意度不少于80的人数为
；
（2）完成表3的
列联表如下，
满意度小于80 | 满意度不小于80 | 合计 | |
六十岁以上老人人数 | 12 | 8 | 20 |
十八岁以上六十岁以下的中青年人人数 | 14 | 6 | 20 |
合计 | 26 | 14 | 40 |
由表中数据，计算
；
没有的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”；
（3）从表3知，用分层抽样方法抽取一个容量为5的样本，满意度小于80的抽取3人，记为
、
、
，
满意度不小于80的抽取2人，记为
、
；
从这5人中任取3人，基本事件是
、
、
、
、
、
、
、
、
、
共10种；
至少有两人满意小于80的是、、、、、、共7种；
故所求的概率是
．
