题目内容
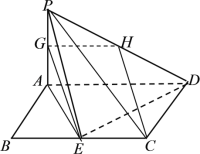
【题目】如图,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)探究在![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由.
,并说明理由.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)连结![]() ,由几何体的空间结构可证得
,由几何体的空间结构可证得![]() ,利用线面垂直的定义可知
,利用线面垂直的定义可知![]() .
.
(2)由(1)知![]() 为腰长为1的等腰直角三角形,结合题意转化顶点可得
为腰长为1的等腰直角三角形,结合题意转化顶点可得![]() .
.
(3)在![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .取
.取![]() 的中点
的中点![]() ,连结
,连结![]() . 易证得四边形EGHC是平行四边形,所以EG//CH,结合线面平行的判断定理可知EG//平面PCD.
. 易证得四边形EGHC是平行四边形,所以EG//CH,结合线面平行的判断定理可知EG//平面PCD.
(1)连结![]() ,∵
,∵![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,同理可得
,同理可得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,且
,且![]() , ∴
, ∴![]() ,
,
又∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
(2)由(1)知![]() 为腰长为1的等腰直角三角形,
为腰长为1的等腰直角三角形,
∴![]() ,而
,而![]() 是三棱锥
是三棱锥![]() 的高,
的高,
∴![]() .
.
(3)在![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .理由如下:
.理由如下:
取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
∵![]() 是
是![]() 的中点, ∴
的中点, ∴![]() ,且
,且![]() ,
,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=![]() AD,
AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG![]() 平面PCD,CH
平面PCD,CH![]() 平面PCD,所以EG//平面PCD.
平面PCD,所以EG//平面PCD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目