题目内容
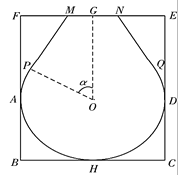
【题目】“金镶玉”是北京奥运会的奖牌设计所采用的式样,喻示中国传统文化中的“金玉良缘”,体现了中国人对奥林匹克精神的礼赞和对运动员的褒奖.它的设计方案,创意十分新颖,突破了以往任何一届奥运会奖牌设计单一材质的传统,又融入了典型的中国文化元素,是中国文化与体育精神完美结合的载体.现有一矩形玉片![]() ,
,![]() 为
为![]() 毫米,
毫米,![]() 为32毫米,
为32毫米,![]() 为
为![]() 的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧
的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧![]() 和线段
和线段![]() 其中优弧
其中优弧![]() 所在圆的圆心为
所在圆的圆心为![]() ,圆
,圆![]() 与矩形的边
与矩形的边![]() 分别相切于点
分别相切于点![]() 以及点
以及点![]() 在线段
在线段![]() 上(
上(![]() 在
在![]() 的左侧),
的左侧),![]() 分别于圆
分别于圆![]() 相切于点
相切于点![]() 且
且![]() .若优弧
.若优弧![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元(
元(![]() ),线段
),线段![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元.记锐角
元.记锐角![]() 镶嵌金丝的总造价为
镶嵌金丝的总造价为![]() 元.
元.
(1)试表示出关于![]() 的函数
的函数![]() 并写出
并写出![]() 的范围;
的范围;
(2)当镶嵌金丝的总造价最低时,求出四边形![]() 的面积
的面积![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)用![]() 分别求出优弧
分别求出优弧![]() 的长以及
的长以及![]() 的长,即可求出
的长,即可求出![]() 的表达式.当
的表达式.当![]() 重合时,
重合时,![]() 取最小.
取最小.
(2)求出![]() ,运用导数的思想,求出
,运用导数的思想,求出![]() 取最小值时的
取最小值时的![]() 的值,进而求出
的值,进而求出![]() 的长,根据梯形的面积公式即可求.
的长,根据梯形的面积公式即可求.
(1)解:如图,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
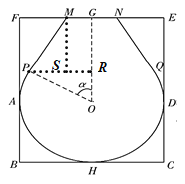
由圆与矩形![]() 相切可知,圆的半径为16,
相切可知,圆的半径为16,
则![]() ,
,
![]() ,
,
因为![]() 与圆相切,切点为
与圆相切,切点为![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以![]() ,
,
即![]() ,
,
![]() .
.
因为优弧![]() 的圆心角为
的圆心角为![]() ,所以优弧
,所以优弧![]() 的长为
的长为![]() ,
,
所以![]()
![]() .
.
考虑临界状态,当![]() 三点重合时,
三点重合时,![]() 为直角三角形,其中
为直角三角形,其中![]() ,
,
![]() ,
,![]() 即
即![]() .
.
(2)解:由(1)知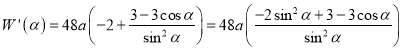
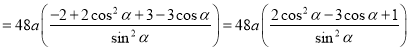 ,
,
其中![]() .
.
令![]() ,得
,得![]() 或
或![]() (舍去).
(舍去).
因为![]() 为锐角,所以
为锐角,所以![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,则
,则![]() 单调递增即当
单调递增即当![]() 时,,
时,,![]() 取最小值.
取最小值.
此时![]() ,
,
![]() .
.

【题目】某市为了调查小区成年居民对环境治理情况的满意度(满分按100计),随机对20名六十岁以上的老人和20名十八岁以上六十岁以下的中青年进行了不记名的问卷调查,得到了如下统计结果:
表1:六十岁以上的老人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 1 | 5 | 6 | 5 | 3 |
表2:十八岁以上六十岁以下的中青年人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 2 | 4 | 8 | 4 | 2 |
表3:
满意度小于80 | 满意度不小于80 | 合计 | |
六十岁以上老人人数 | |||
十八岁以上六十岁以下的中青年人人数 | |||
合计 |
(1)若该小区共有中青年人500人,试估计其中满意度不少于80的人数;
(2)完成表3的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”?
的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”?
(3)从表3的六十岁以上的老人“满意度小于80”和“满意度不小于80”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取3人,求至少有两人满意小于80的概率.
附: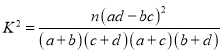 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |