题目内容
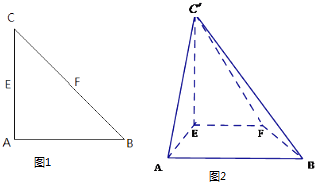
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场. 为安全起见,需在
地带开设儿童游乐场. 为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?

【答案】(1)防护网的总长度为![]() (2)
(2)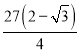
【解析】试题分析:(1)首先根据直角三角形中![]() ,得到
,得到![]() ,结合
,结合![]() ,由余弦定理可求得
,由余弦定理可求得![]() 的值,利用勾股定理证得
的值,利用勾股定理证得![]() ,由此证得三角形
,由此证得三角形![]() 为等边三角形,从而求出周长.(2) 设
为等边三角形,从而求出周长.(2) 设![]() ,根据
,根据![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍列方程,求得
倍列方程,求得![]() 的值,在
的值,在![]() 中利用正弦定理求得
中利用正弦定理求得![]() 值,两个值相等,由此求得
值,两个值相等,由此求得![]() 的值.(3) 在
的值.(3) 在![]() 中,利用正弦定理求得
中,利用正弦定理求得![]() 的值,利用三角形面积公式写出面积的表达式,并利用三角函数值域来求面积的最小值.
的值,利用三角形面积公式写出面积的表达式,并利用三角函数值域来求面积的最小值.
试题解析:
(1)![]() 在
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
由余弦定理,得![]() ,
,
![]() ,即
,即![]() ,
, ![]() ,
,
![]() 为正三角形,所以
为正三角形,所以![]() 的周长为
的周长为![]() ,
,
即防护网的总长度为![]() .
.
(2)设![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
从而![]() ,即
,即![]() ,由
,由![]() ,
,
得![]() ,
, ![]() ,即
,即![]()
![]() .
.
(3)设![]() ,由(2)知
,由(2)知![]() ,
,
又在![]() 中,由
中,由![]() ,得
,得 ,
,
![]()
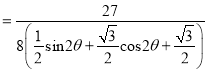
![]() ,
,
![]() 当且仅当
当且仅当![]() ,即
,即![]() 时,
时,
![]() 的面积取最小值为
的面积取最小值为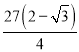
![]() .
.

【题目】在2015﹣2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表(注:表中分数 ![]() ,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根据统计表的信息:
(1)从上述比赛中等可能随机选择一场,求甲球员在该场比赛中投篮命中率大于0.5的概率;
(2)试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率;
(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率超过0.5的场次,试写出X的分布列,并求X的数学期望.